LEARNING THE ARCHITECTURE OFDEEP NEURAL NETWORKS

其中我感觉比较重要的一句话：

It is well known that two neural network layers without any non-linearity between them is equivalent to a single layer, whose parameters are given by the matrix product of the weight matrices of the original two layers.

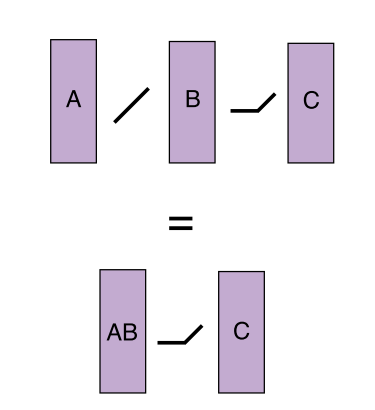
如上图所示，其中直线代表线性 折线代表非线性

就是我们每一层的网络的参数的个数  就是每一层节点的个数为ni

目标函数为：

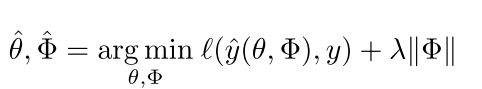
把这种学习方法叫做 Architecture-Learning (AL)algorithm 就是不是以模值L1L2来约束了 而是以参数来约束

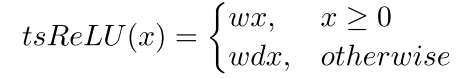
这就是它们定义的激活函数  

This reduces to the usual ReLU for w = 1 and d = 0. 也就是非线性的激活函数 For w = 1 and d = 0 it behaves similar to ReLU, while for d = 1 it reduces to the 

identity function. 

网络中每一层的各个w不一样 但是每一层的d都一样 要么是0要么是1  也就是要么这一层是线性的要么是非线性的  所以d是控制网络depth的 w是控制width的

width是控制每一层的参数的个数 而depth是控制网络层数的

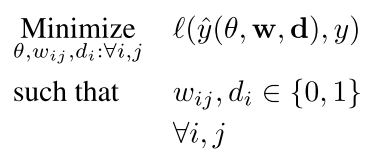
因为我们的这几个参数w和d要么是0要么是1  所以我们的问题变成了ILP问题（binary）

we require a method to learn binary parameters for w and d. To this end, we use the regularizer given by w(1 − w) (or d(1 − d))

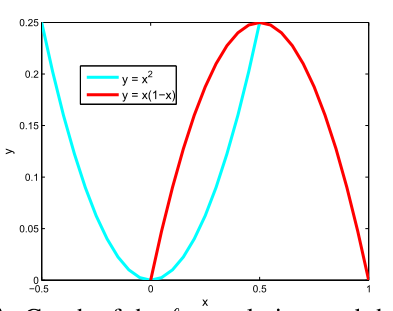 这种性质很好

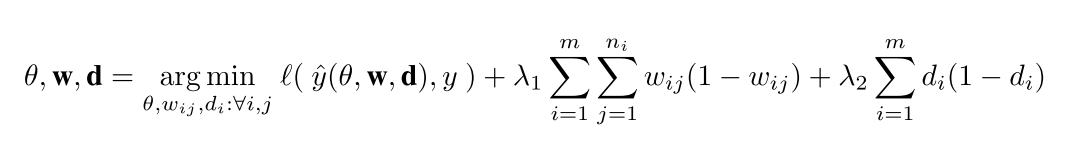
这样梯度就好求了  我们最后做一个约束

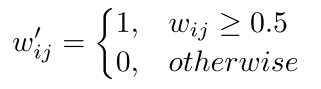
所以把ILP变成了一个简单的问题

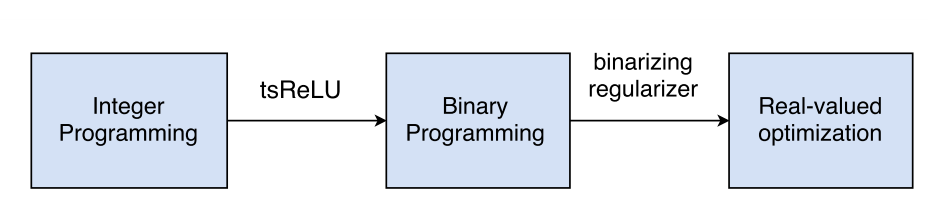
光有一个这样的还不行 因为上面的那个公式只是让w和d趋于0和1  但是并没有对最后的模型的复杂度进行约束 所以我们需要加入一个约束来定义模型的复杂度

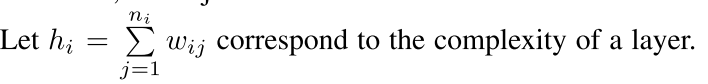
the model complexity term is given by

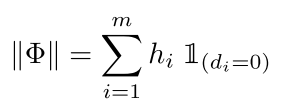
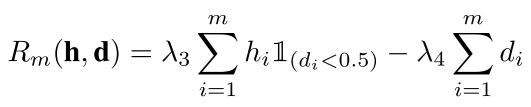
把这个和上面那个公式结合起来就是我们最后的结果了