这个文章是对传统的VI的一种改进，VAE里面也可以用这个进行改进，取得了不错的效果

发在ICML15上面的

介绍里面有一点很重要：

Variational inference requires that intractable posterior distributions be approximated by a class of known probability distributions, over which we search for the best approximation to the true posterior. The class of approximations used is often limited, e.g., mean-field approximations, implying that no solution is ever able to resemble the true posterior distribution. This is a widely raised objection to variational methods, in that unlike other inferential methods such as MCMC, even in the asymptotic regime we are unable recover the true posterior distribution.

也就是以往对后验的估计都是一种近似的或者MCMC的方法，如mean-field，但是这种估计都会损失很多信息，比如mean-field会假设这个东西是独立的等等

传统的VI，是这样的一个形式

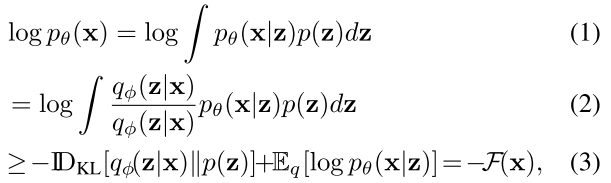
一般上面3的那个F被称为F or as the evidence lower bound (ELBO).

我们在VAE里面已经知道那个隐含状态是Z 然后现在我们就继续处理，有一种模型叫作Deep Latent Gaussian Models

which are a general class of deep directed graph- ical models that consist of a hierarchy of L layers of Gaus- sian latent variables z l for layer l. Each layer of latent vari- ables is dependent on the layer above in a non-linear way, and for DLGMs, this non-linear dependency is specified by deep neural networks. The joint probability model is

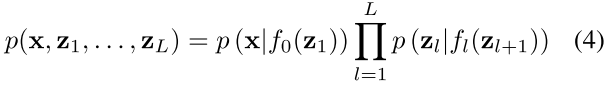
所以我们可以现在把这个隐含层也给弄成好几个的，这就是Normalization Flow

A normalizing flow describes the transformation of a prob- ability density through a sequence of invertible mappings. By repeatedly applying the rule for change of variables, the initial density ‘flows’ through the sequence of invert- ible mappings. At the end of this sequence we obtain a valid probability distribution and hence this type of flow is referred to as a normalizing flow.

也就是对概率密度进行不断的转化，使之能逼近更为真实的密度空间

假设z'=f(z) 那么我们有

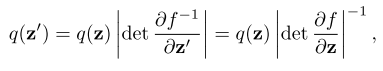
其实这个是多元分布的一种，我们知道在单变量的时候，假设y=f(x) 那么x有密度函数p 即分布为p(x) 那么我们知道在一个微分的条件下，p(x)dx就是这个x在这个极小值dx下的

概率，然后这个y=f(x)这种单调转化 则在y那个极小空间里面概率应该一样 也就是p(y)dy=p(x)dx  因此我们有p(f(x))=p(x)/f'(x) 这个就是单变量的函数转化密度方程

对一个变量进行函数转化后的概率分布

然后在多变量的情况下这个就可以变成上面的那个式子了 也就是行列式的形式

进行了K次转化后，我们有

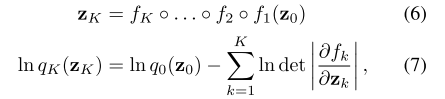
上面的公式（7）是这篇文章最重要的一个部分，也就是对上面公式（3）中的那个东西的变化，我们现在需要的就是这个东西

作者提出了几个这种转化的东西，其中之一便是：

可以看到可以很好的应用在我们的VAE任务上面，有个初始值，然后不断的进化，就行了

这篇文章写的很棒！！！