Improving Variational Auto-Encoders using Householder Flow

Max Welling是VAE的鼻祖

首先，这个文章是上面那个文章的延续，只不过用了更好的flow，我们为什么要在VI里面用这个flow就不说了，见下面

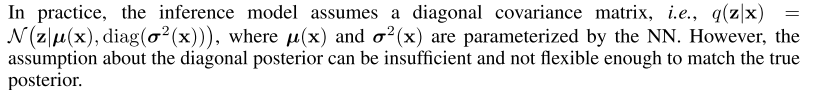
反正最后的形式是

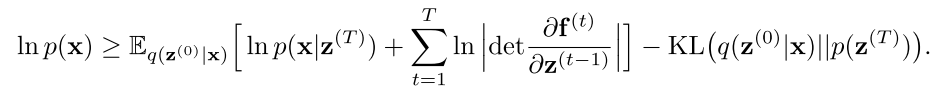
然后就是现在的一些Normalization flow的形式，

可以看到其中有一个是 general normalization flow 还有一个是volum preserving flows 上面那个文章就是用的第一种吧应该

然后这个文章主要是研究第二个，他们的差别就是雅各布行列式怎么被计算的，但是volume preserving的那种要保证所有的行列式都是1  因此在上面那个式子里面保证了左边的那个det是0（ln后）

然后我们看看作者怎么用Householder Flow来计算的，

--------------

假设我们的方差矩阵式full的  那么它可以被分解成

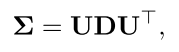
而我们知道一个正交矩阵的雅各比行列式为1    所以我们有 for

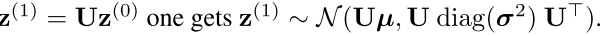
因为我们最后就是为了得到一个Z（t）使之能符合右边的那个分布Udiag()Ut 所以我们的任务就是怎么找到这么一组变换，使之能够成为上面的那个

然后我们有一个公里

所以

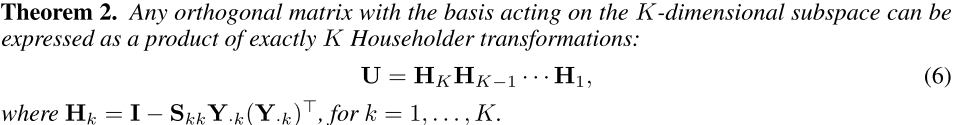
好了 现在我们可以看看在VAE里面怎么去找这个flow了

我们的这个转换就是这个householder转化，

其中的每一个转化中，根据公式6 我们知道SYYT就是上面式子中的右部分，而且k=1 

在VAE里面，这个v（x）也是由我们的VAE的encoder提供的，我们提前设定好一个t 然后用VAE产生一系列的V  就可以得到了

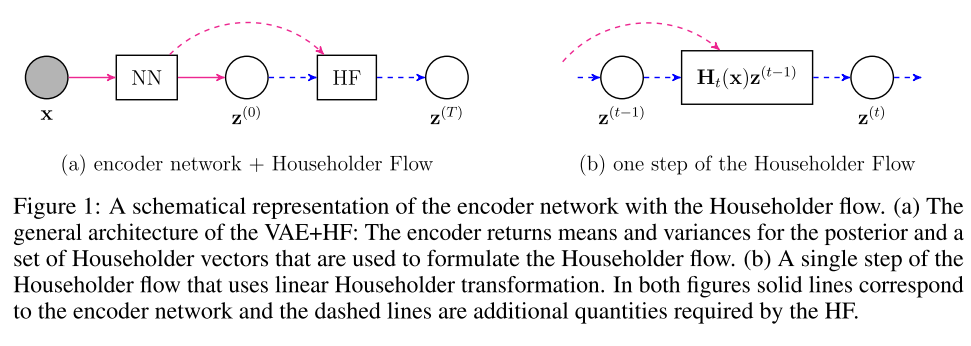
然后是实验

可以看到确实这个z很像真实的点了

=====================================

而且有一个重要的性质就是  

这个东西放上去 因为是Householder的，也就是只有协方差的一些东西，添加的变化都是正交的，因此在VAE的求导函数里面所有的东西都没有变，即目标函数还是那样写，只不过我们的那个隐变量Z变了，变成了我们设计的那个转化后的东西