今天看一个关于扩展结构的方法,其中最重要的原理就是让模型在Test time的时候不仅仅依靠生成更多tokens,而是靠迭代的方法,来取得效果的提升。
https://arxiv.org/pdf/2502.05171
背景:
其实很早之前我就想过一个扩展计算能力的方法,如下:
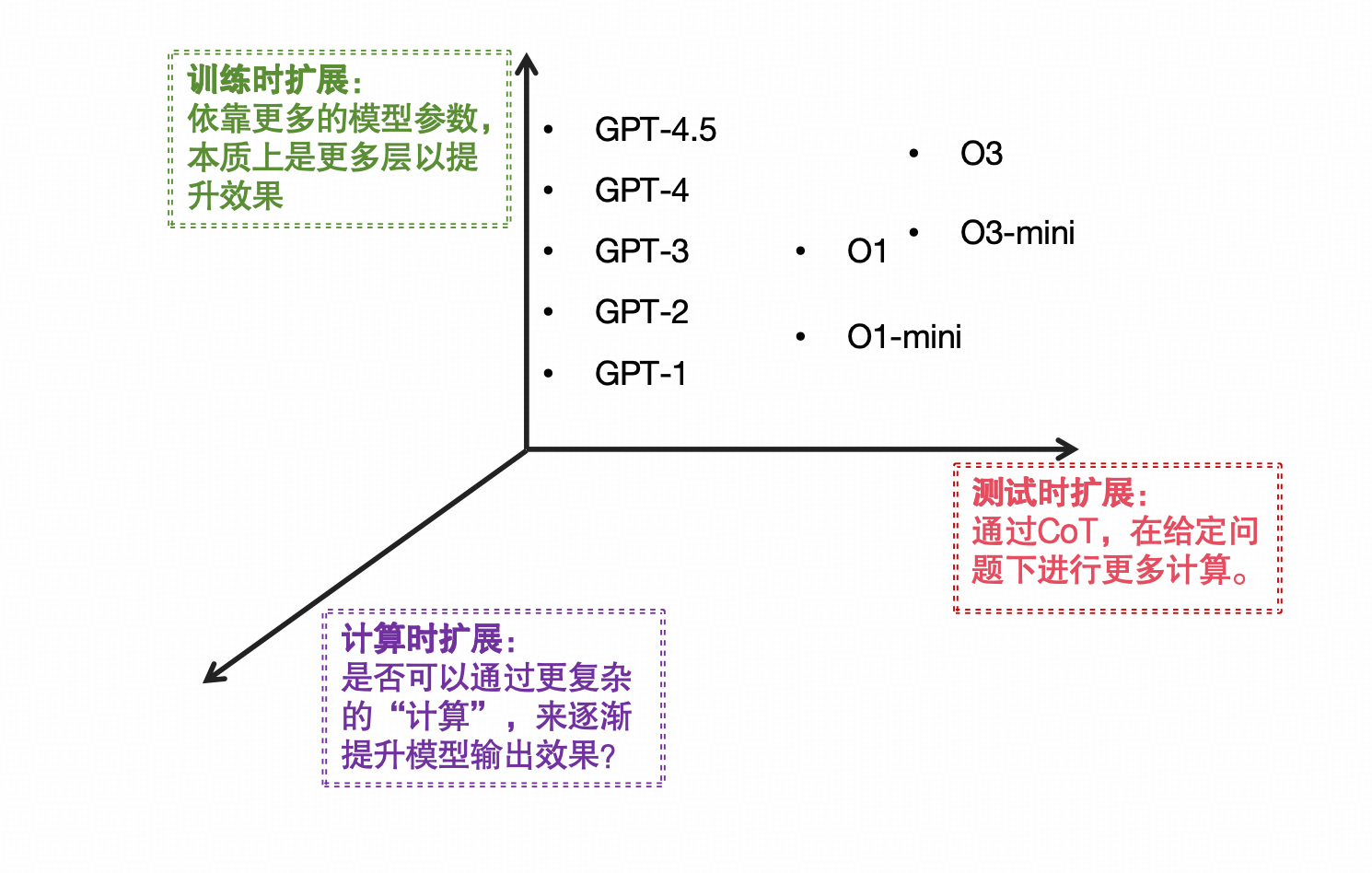
因此我们看看这个工作的主要做法:
方法

直接说方法:
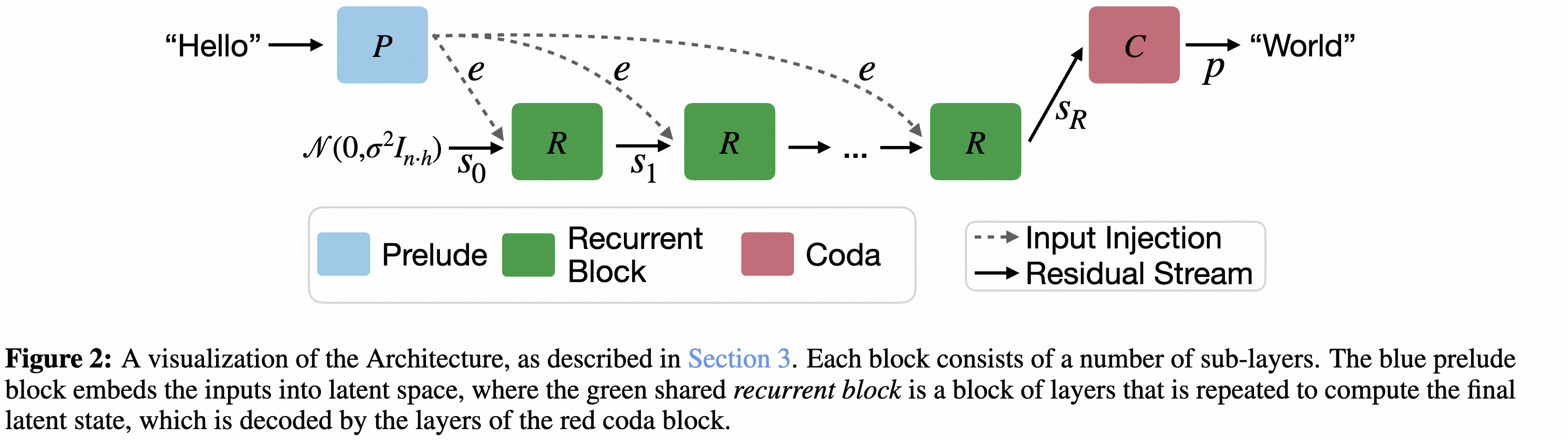
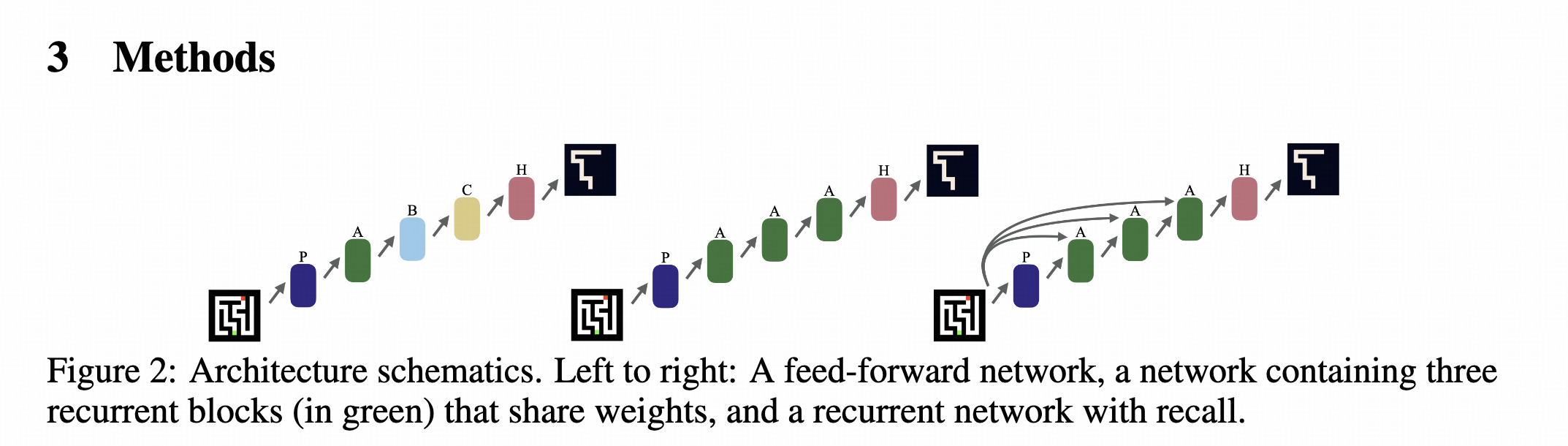
这个图可以非常清晰的看出来,这个方法最重要的其实是把从P到C的过程中(传统Transformer里面应该就是直接输出了)加入了一个循环的过程,循环次数越多,效果越好。
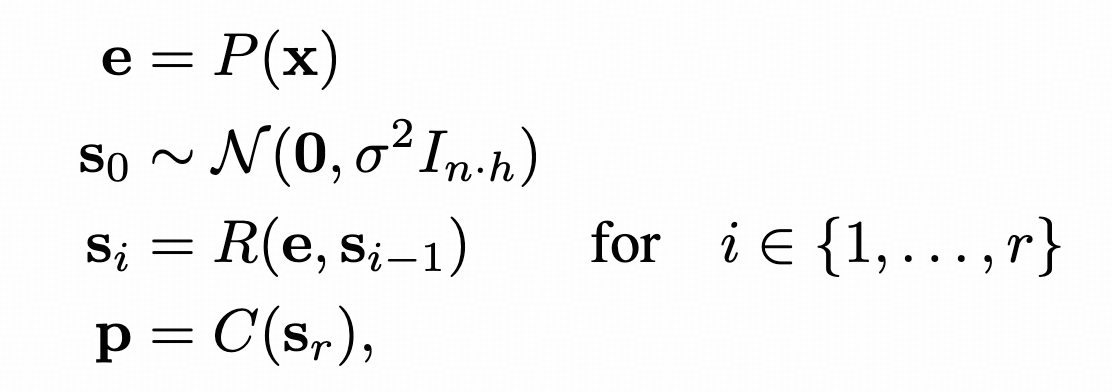
可以看到中间的过程就是一个循环网络,只不过这个的输入是固定的e,也就是前面Transformer的输出。
实际的时候,中间循环的步数是可以控制的,如下所示:
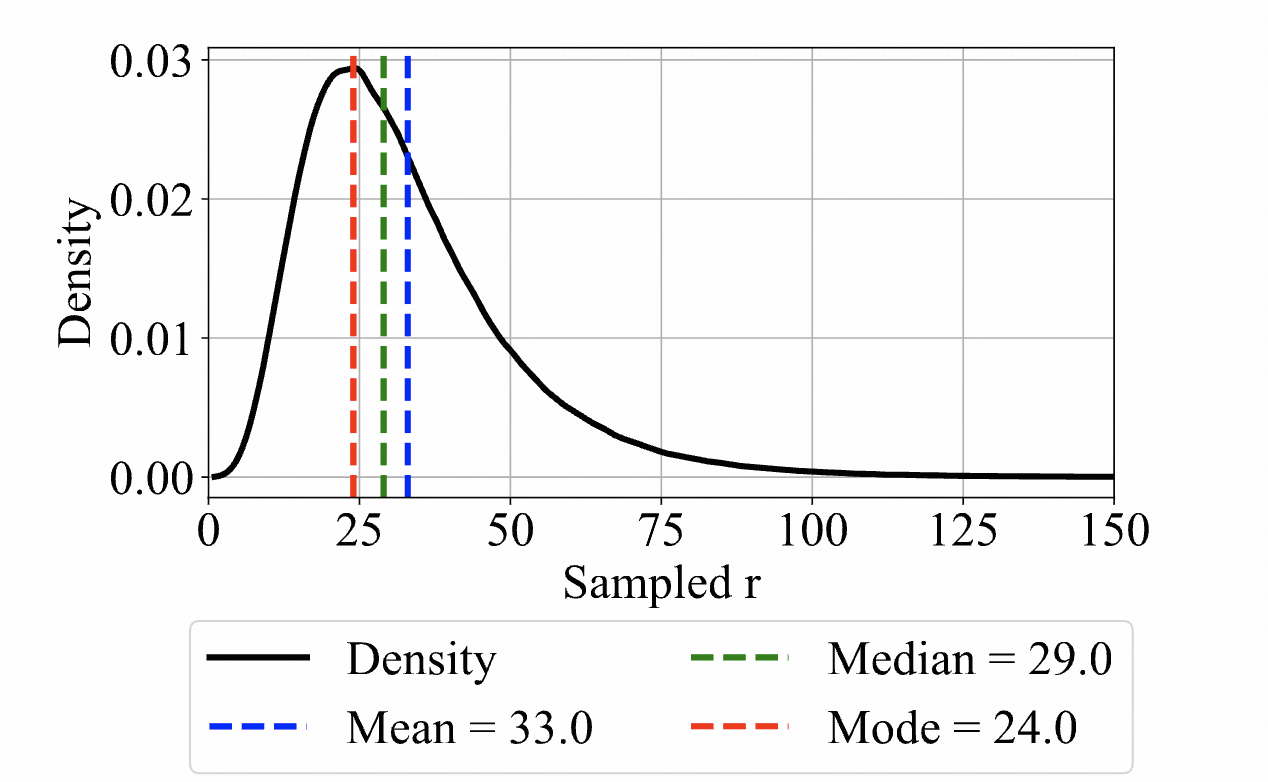
用了一个
log-normal Poisson distribution
结果:
最后的训练效果如下:
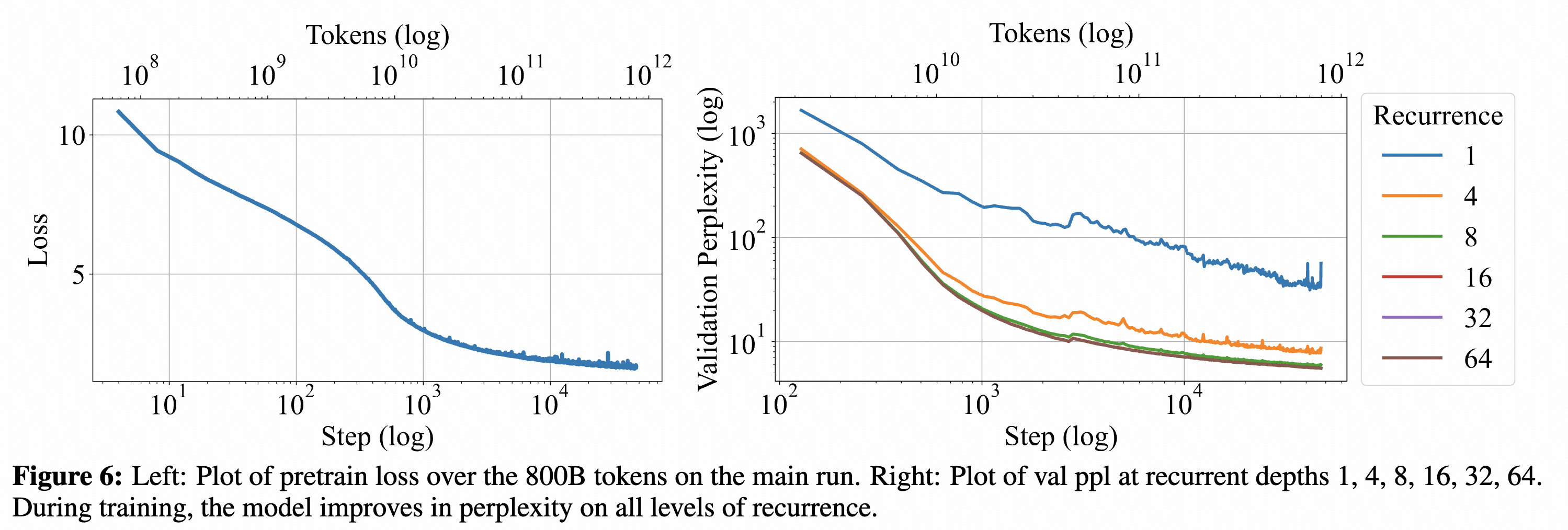
可以看到loss确实会随着r(即循环次数)的增大而增大。
但是从最后的效果来看,有一个很奇怪的地方,就是循环16次和循环32次的效果几乎没有差距,见下面:
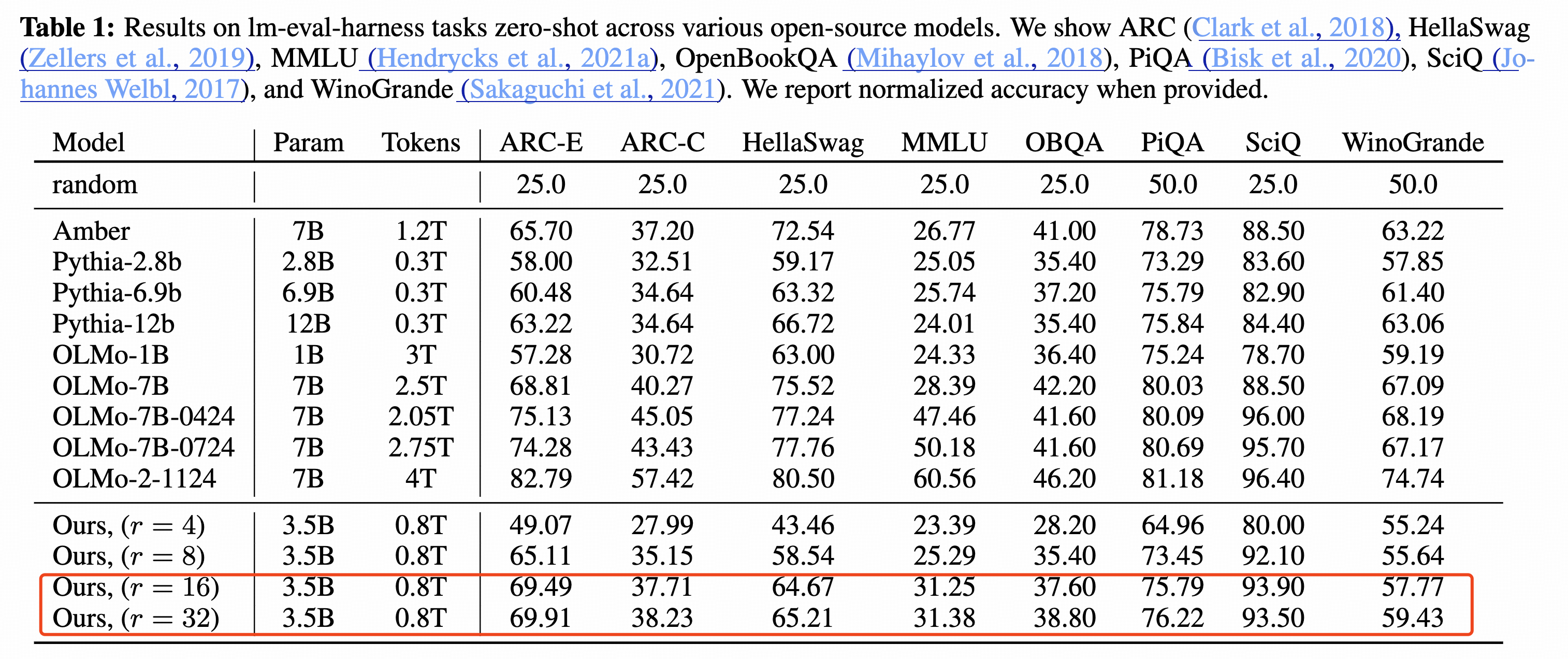
个人猜想:
这个工作只是一个原型,是为了验证效果而提出的,但是并没有一个很好的去解决这个循环次数(什么时候应该循环,应该循环几次)。
其实和固定的Transformer layer的方法一样,这一类的工作应该算是类似传统Scaling的方法,即有一个先验:传统Scaling是定义多少层,这个工作是定义循环多少次。并且由于在训练过程中并没有一个策略去让模型自己去发现应该是尽量少的循环还是尽量多计算(而是一个固定的),因此这种方法模型会“偷懒”,即有可能最后面的循环是非常“冗余的”。可能这种固定计算的方法都会有冗余性 https://arxiv.org/abs/2403.03853 (之前对Dense模型的研究发现最后几层会有很强的冗余性)
而对比CoT的方法,这种方法可能效率更低,因为CoT可以根据词汇化(verbalizing)来自己生成EOS结束生成,因而会更加动态。未来可能有希望的方法是:有一种先验,即计算是需要消耗能量的,如何设计一个在预算内的Budget去减少计算的依赖,以减少能量的消耗,在训练和推理的时候都是会以最低的成本得到结果。
为什么RNN更好?
我们可以看一个更早的工作:https://arxiv.org/pdf/2106.04537
直接把结论(o1整理的)放在这里:
这篇文章的主要内容是探讨递归神经网络(Recurrent Neural Networks, RNNs)是否能够从简单问题的学习中推广到更复杂的问题,即能否“学习算法”。作者们的研究发现,递归网络在训练时仅需学习解决简单问题的方法,在测试时增加推理次数(迭代计算),就能够解决更复杂的问题。
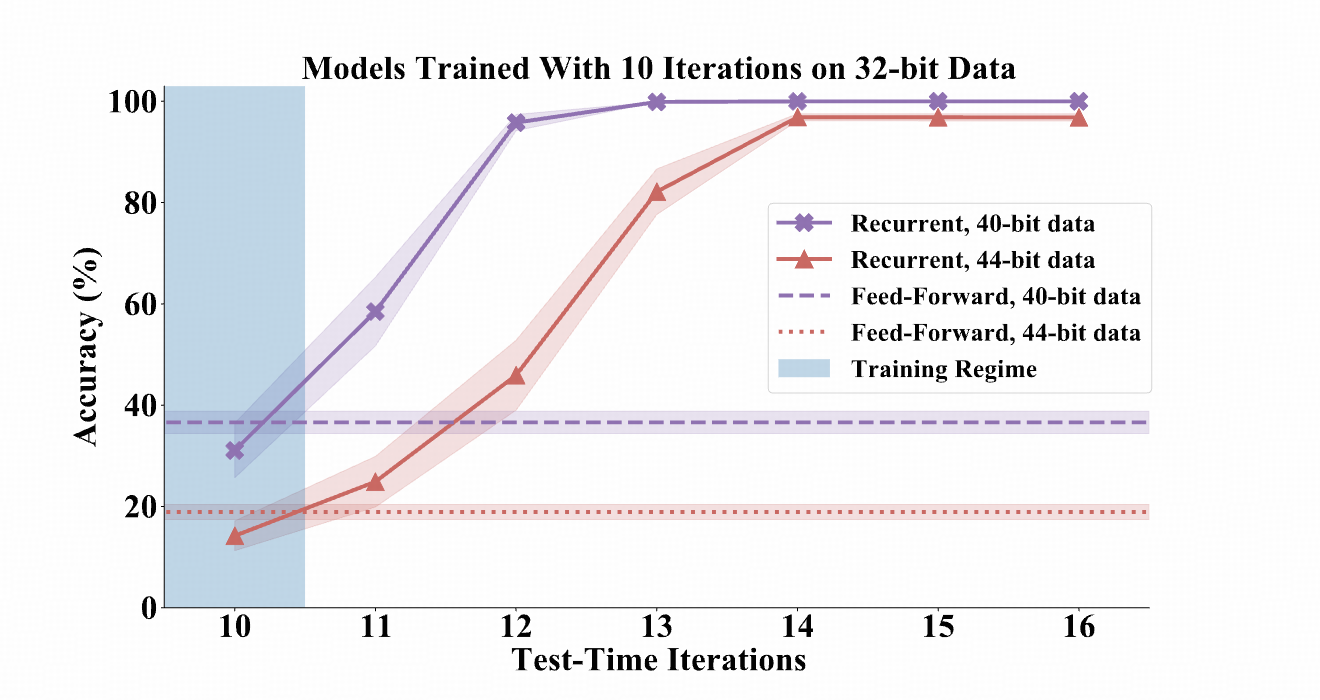
主要研究内容
问题背景
人类可以通过更长时间的思考,将在简单问题中学到的推理策略应用到更复杂的问题上。例如,一个人学会解决小迷宫后,可以用相同的方法解更大的迷宫,只需花费更长的时间。
计算机通常通过算法来实现类似的能力,但传统**前馈神经网络(Feedforward Neural Networks, FNNs)**的计算层数是固定的,因此无法适应更复杂的问题。
研究目标
研究递归网络(RNNs)是否能通过增加测试时的递归迭代次数,从简单问题推广到更难的问题。
研究哪些任务适合这种推广方式,并评估递归模型与传统前馈模型的性能差异。
实验任务
**前缀和(Prefix Sum)**计算:给定一个二进制字符串,计算其前缀和(mod 2)。
迷宫求解(Maze Solving):给定一个迷宫图,找到从起点到终点的最短路径。
国际象棋残局解法(Chess Puzzles):预测最佳下一步走法。
实验方法
训练:在简单问题(较短字符串、小迷宫、低难度棋局)上训练模型,限制递归网络的最大迭代次数。
测试:在更复杂的问题(更长字符串、大迷宫、高难度棋局)上测试,允许递归网络使用更多的迭代次数。
对比基线:前馈神经网络(FNNs)在相同任务上的表现。
主要发现
前缀和计算:模型在计算过程中逐步累积前缀和,与人类直觉的计算方式相似。
迷宫求解:模型在每次迭代中逐渐收缩解空间,找到更短的路径。
国际象棋残局:模型在多个迭代中逐步调整最佳走法的置信度,类似人类的思考过程。
递归网络在训练时的推广能力有限,但在测试时增加迭代次数后,可以显著提升性能。
递归网络在前缀和计算、迷宫求解和国际象棋残局预测任务中都比前馈网络更擅长从简单到复杂的推广。
递归网络可以表现出类似算法的行为,例如:
讨论与意义
研究表明,递归网络能够学到可推广的推理过程,而不仅仅是对训练数据的记忆。
这与人类的思维方式类似,即在简单任务上练习后,通过更长时间的思考解决更复杂的问题。
未来可能可以用神经网络代替手工设计的算法,例如国际象棋AI可以不依赖蒙特卡洛搜索,而是完全靠递归网络的学习能力来推理最佳走法。
总结
核心结论:递归网络可以通过增加推理深度,在测试时推广到更复杂的问题,表现出类似算法的行为。
对比前馈网络:前馈网络无法在相同训练数据下泛化到更复杂的问题,而递归网络可以。
未来应用:可能可以利用递归网络来构建更智能的AI,解决传统需要手工设计算法的问题,例如游戏AI、路径规划、数学推理等。
如果你对某个部分需要更详细的解释,或者想看某些实验数据,可以告诉我!
还有一个后续的工作,说明RNN可以“泛化到更复杂的策略中”
这个也是看解迷宫的问题,对比的模型也是FFN和RNN以及变体
回复列表: