一般的假设我们的输入是x(n维) 然后我们有一个隐变量z 是m维的 我们假设 additional parameters α that are fixed.
一般的 bayes那一套就是
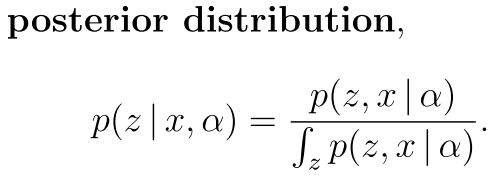
也就是对一个隐含变量的后验就是它的先验的一些做法
有时候 为了求得这个隐变量 需要大量的计算 就像上面的那个 因为分母上面的积分 所以我们的计算很辛苦
现在我们可以考虑 将这个东西换一下 换成一个可以计算的 要不然intractable
其中好多都是对这个分母在mcmc上面就是估计一个分布 然后让另外一个分布来逼近她 其实也是一个求期望的过程
现在换一个变分模型 就是假设隐变量是一个模型产生的
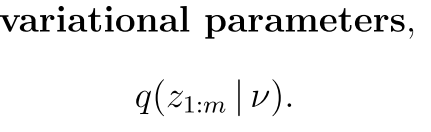
Then, find the setting of the parameters that makes q close to the posterior of interest.
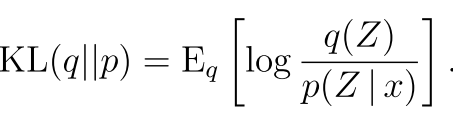 就是输出的模型是p 我们这个变分的模型是q
就是输出的模型是p 我们这个变分的模型是q
--------------------------------------------------------------------
我们再看看这个对可观测值求期望的过程
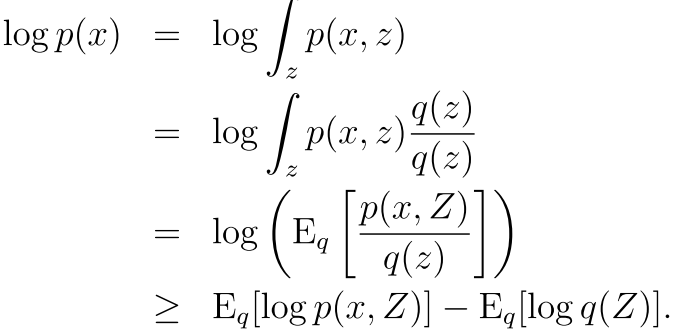 ----(1)
----(1)
可以看出来 最后我们想让这个期望最大化 也就是让这个p(x,z)最大和右边的最小 右边的是熵 也就是 我们要找到一个q 使
这个q的不确定性最小 也就是隐变量在这个model(q)下面比较确定而且在和x相关之后又不确定了
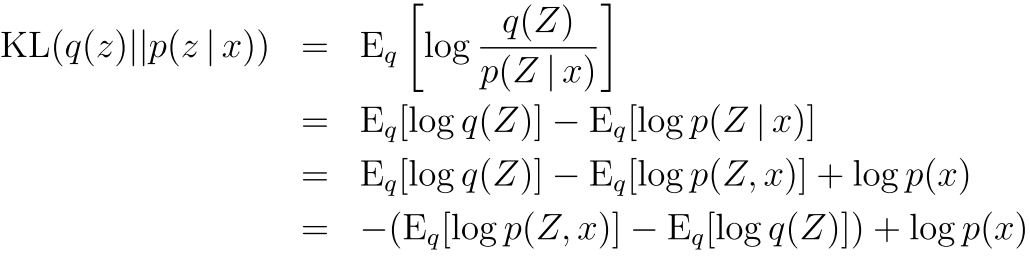
可以看出来有几点 就是为了让我们的kl距离比较小 然后logP(x)和那个变分模型q没有关系 所以我们可以只管前一部分
所以 让kl最小等同与让最下面那一行左边最大 这就是跟上面那个式子(1)一样了
--------------------------------------
mean-field variational inference
假设我们可以把隐变量分为这样的
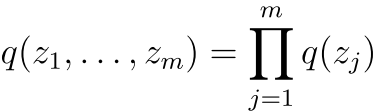
然后我们可以看到这是一个假设每一个隐变量都独立的假设
We will use coordinate ascent inference, interatively optimizing each variational
distribution holding the others fixed.
假设我们的数据是下面这样一个chain rule产生的 也就是
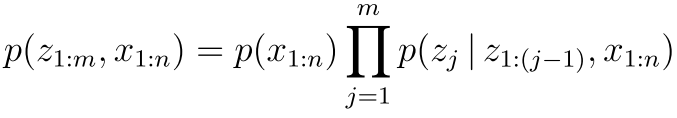
我们现在可以看到 这个东西是有点类似马尔可夫链的性质
然后我们将上面那个elbo里面的其中一项变分的熵给找出来
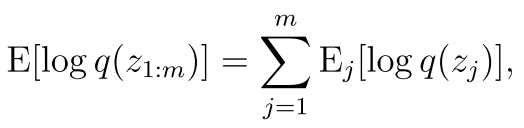 意思就是分开了 因为我们假设独立么
意思就是分开了 因为我们假设独立么
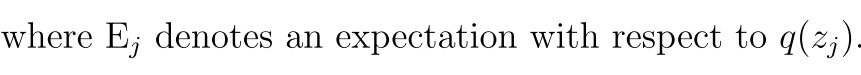
现在我们的ELBO变成了
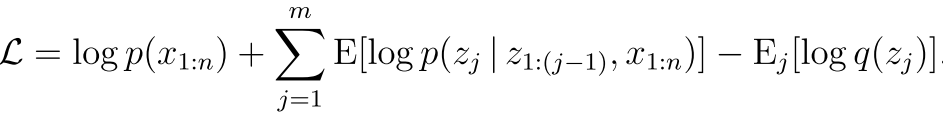
然后我们把上面这个弄成期望的形式
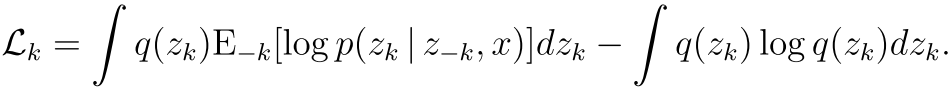
就是加了一个q(Zk)然后求期望 还是跟原来一样 只不过这个是对每一个k了 是一个k的函数
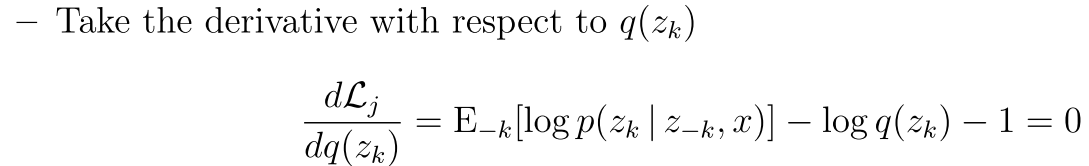
所以达到最优解的时候
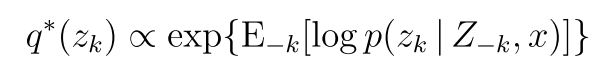
由于我们的分母 也就是上面式子右边和我们的zk没有关系 所以可以表示为
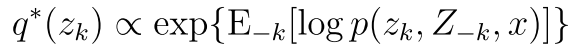
最后我们可以看到一个例子

也就是可以用这个多元分布来模拟这个东西
哈哈 变分就是这么简单
=====
假设有一个指数函数族人
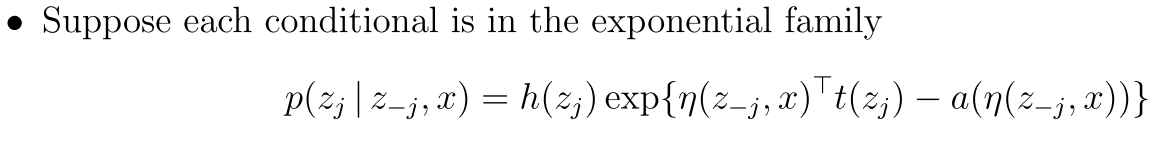

回复列表: