![]()
这个文章不错 可以看一下
还有一个教程也不错
![]() An Introduction to Conditional Random Fields.pdf
An Introduction to Conditional Random Fields.pdf
=============================================================================================
好了 现在我们言归正传,开始今天的题目
条件随机场以前一直知道个皮毛。我最近才开始看的仔细 现在给介绍一下
首先 CRF主要是为了序列标注的,这个应该是我们所有人应该知道的一个最基本的东西,在深度学习领域,大部分都是分类,在那个领域要是想用序列标注就得借鉴NMT的东西,也就是encoder-decoder那样,但是deeplearning是非常data-hungry的,所以我们在一般的任务上面还是老老实实的传统特征工程就行了。
我还是就这Sutton的tutoral开始讲吧
首先,什么是无向图,无向图是一种图的结构,各个顶点之间没有联系。但是我们可以求出来一个概率,对于这个图,这个图上的各个节点都是相当于传统机器学习里面的
变量(一个个特征),所以他们整体在一起就是一个样本,但是我们知道,各个节点和特征之间肯定不是完全独立的,各个特征之间存在着一系列的关系,我们用无向图去刻画这种关系,然后,对于这个图,我们不仅仅把这个变量(特征)给糅合进去,还把最后的输出也糅合进去了,假设输入是x,输出是y,我们现在把他们都表示在一个图里面。
然后,对于某一个x给定后,我们就可以看看这个整体的概率是多少了。也就是
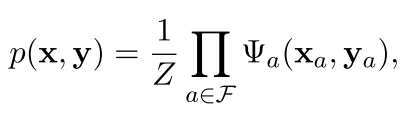
其中的f是在这个图中间各个独立的模块(subset)。
然后对于其中某一部分,我们定义的这个叫做local function 也就是局部函数,就是为了把这局部的东西映射到一个概率上
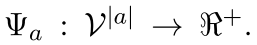
These functions are also called factors or compatibility functions. 也就是因子
现在,还要对整个概率进行归一化
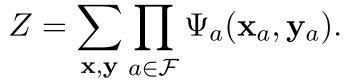
注意 现在是最基本的时候,在上面的这个分母z里面,因为是要遍历所有可能的x和y 所以一般是intractable的,但是有很多近似方法已经被提了出来。
而对于这个局部函数,一般都是用指数函数家族来刻画
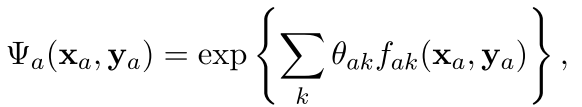
这个就不用多说了吧,特征工程里面的那一套,
---------------
现在看看什么是马尔可夫网络 也就是 Markov network 其实也就是无向图的另一种说法,也就是上面的那个公式一样,也就是我们现在对这个样本中的任意一个向量拿出来,它只跟它周围的变量有关,也就是和它有链接的变量有关。
用一个定理来说明:Hammersley-Clifford:Suppose p is a strictly positive distribution, and G is an undirected graph that indexes the domain of p. Then p is Markov with respect to G if and only if p factorizes according to G.
也就是我们的一个无向图是可以这样的,整体的概率是可以分解为其中小部分的。
我们看看这样将一个大的概率分解成小的概率的好处
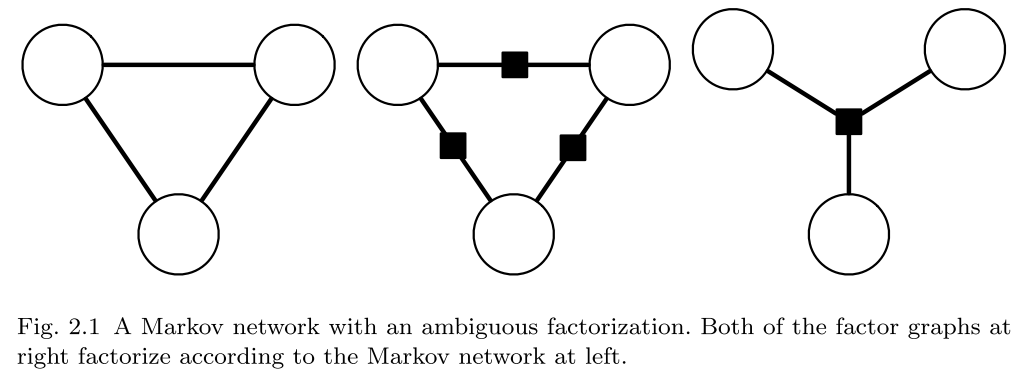
where p(x1, x2, x3 ) ∝ f(x1, x2 )g(x2, x3 )h(x1, x3 ). This second model family is smaller, and therefore may be more amenable to parameter estimation.
也就是第一个图可的概率可以用中间那个因子来表示出来 其中的黑色方框是表示一个factor 也就是一个因子
---------------------
虽然无向图中的factor不能有概率的解释,但是有向图就可以了
在有向图里面 是这样表示整体的概率的
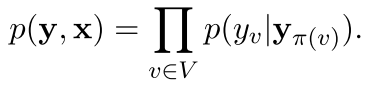
其中v可能就是指其中输出的某一维 pai(v)表示和这个输出的点的相关的 可能全部是输入
所以他们的差别就是在这个里面不是统一的构造了,而是单独的把输入拿出来,生成这个输出
=======================================生成式和判别式的差别========================================
我们首先拿分类任务来举例子。在分类任务里面,有一个很好的简单方法就是朴素贝叶斯,他的结构如下:
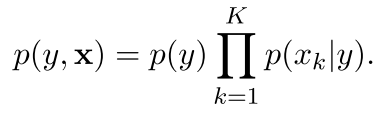
表示成图的意思 就是下面这样
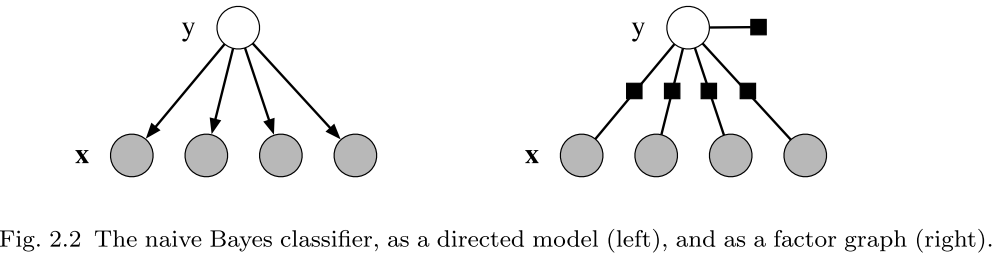
其中左边是他的一个结构表达,右边是factor的表达,可以看到其中某个factor(右上角那个黑点)和其他的factor是不相关的 注意右边是无向图,所以还是有独立性假设
然后和这个对比,我们看看判别式里面的一个小兄弟:逻辑斯谛回归(有时候也就啊哦做最大熵分类器)
它的结构是这样的
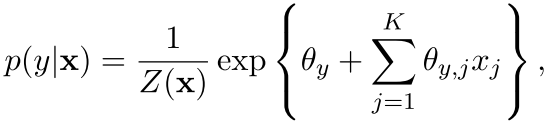
![]()
可以看出来这个就是以前在ESL里面讲logistic regression的那个表达式么
但是其中有一个\theta_{y}是bias,但是现在咱们还是好好的表达一下吧,就是把上面的特征换掉,变成了这样
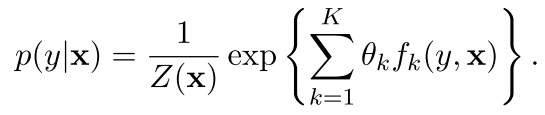
K是表示特征模板的个数
在序列标注任务里面,有一个是NB的扩展,那就是HMM,他的表达就是这样
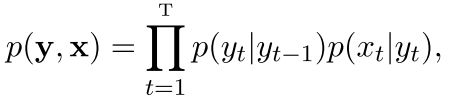
其中的马尔可夫性体现在,虽然现在还是y生成x,但是现在是一个序列了,也就是yt也有多个,而且每生成一个,xt不会怎么变,但是yt会有一个转移概率,这个就是马尔可夫
!!!!前方高能!!!
我们在图模型的视角下,生成式模型主要是一个联合的分布,也就是p(y,x),而且主要是输出(隐变量)怎样以概率输出输入(x).但是判别式模型主要是将他们联合在一起进行构建,而且最后的概率是由输出判别出输出的概率
1)对于判别式模型来说,根本不需要去构造p(x)[也就是我不需要知道任何关于x的分布,不管它是单独的p(x)还是marginal的p(x|y)],因为对于这个x在我们的任务中更本不需要,我们只是想求某一种y的概率罢了
p(x)非常难以刻画,而且各个x之间可能有很大的联系(在隐马里面和NB里面有这个独立性假设,也就是这个x只跟当前的y隐变量有关)
判别式模型的主要好处就是它把这种独立性假设给舍弃了,而且可以包含很多有用的,各种各样的可能有交叉的特征(在各个x之间或者y之间)
还有一种纯从概率的角度理解他们的不同的是下面这个:
对于生成式模型,假设是这样
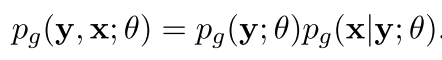
我们可以重新改写为
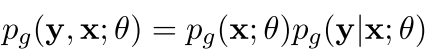
-----------------(1)
现在我们把p(x)用一个生成式的东西表达出来,就如下
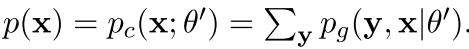
而且还有
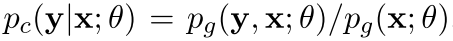
好了现在判别式的写成一个概率只和的形式就是下面这样
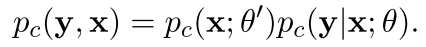
-----------------(2)
比较1和2 可以看出来参数有所变化 呵呵呵呵呵呵呵呵呵呵呵呵呵呵呵呵呵呵
作者说: it can be seen that the conditional approach has more freedom to fit the data, On the other hand, this added freedom brings about an increased risk of overfitting the training data, and generalizing worse on unseen data.
但是同时我们也知道,不是有一种模型是万能的,就是生成式模型也有他的好处,它比较善于刻画隐变量,而且,由于它对输入也建模了,所以p(x)可以当作一个平滑的函数,来处理
分布的不均匀
最后 还是统一的表述一下几个模型在一个图里面吧
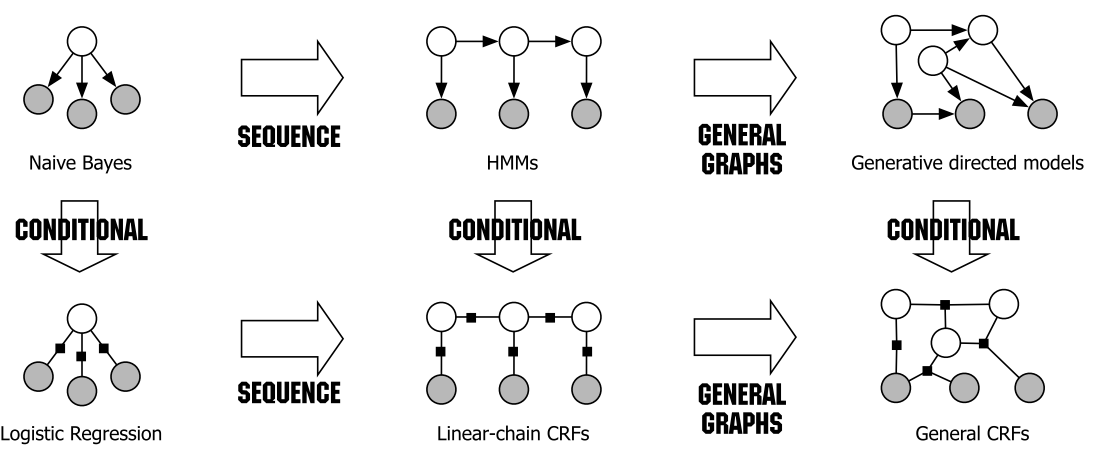
我们知道,后来的两个在图里面是因为以前序列的两个只是考虑输出(隐变量)之间的连续的这种关系,假设还是有点强,就是一个序列是由线性的可分的独立factor构成的,
但是在通用图里面,序列中任何一个隐变量可以和以前任意一个隐变量或者输出连接在一起。
============================================================================================
线性的CRF
首先还是上公式:
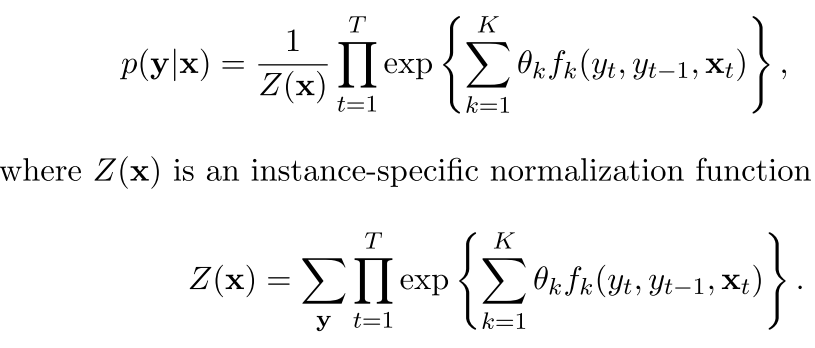
注意在实际中xt是可以有很多个的,包括以前好几个变量如下图(所以上面的公式里面xt加粗了)

现在看看大大的CRF(General CRFs) 因为这种CRF的刻画能力真是牛逼
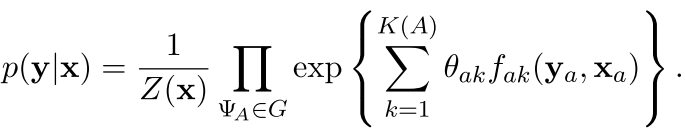
其中的
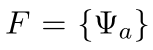
是the set of factors in G,也就是图中的因子,在线性的里面就是直接从前刷到后面,但是在通用的里面是一个factor了
To denote this, we partition the factors of G into C = {C1, C2, . . . CP }, where each Cp is a clique template whose parameters are tied.
==========================好 现在看到了生成式和判别式的一些差别,现在我们来看看具体实施的时候 CRF有什么要注意的地方--------------------
在我们的CRF公式里面,特征函数是有下面的这个形式:
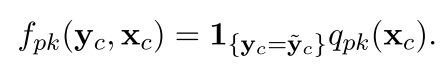
也就是我们的特征函数首先是分成两部分,第一部分是最后的隐变量,隐变量之间的关系,比如上一个变量是NN,当前的是PERSON。这个东西一般是确定的,我们要关心的就是下一部分的q,也就是和当前输入有关的。
这个q叫作obesevation functions 一般的这种函数有:当前词,当前词大写,当前词的长度是1等等等等。
而且一般的情况下,这种方程都是二值的,也就是很长很长的一个大向量,然后每一维代表这个到底出现了没有。
================================术语================================
无向图也称作马尔可夫网络,或者吉布斯分布
贝叶斯网络也是有向图的一种简称,但是一般还是叫后者的比较多
参数学习
现在我们有了模型,那么我们开始对模型中的参数进行训练。
还是一般的很多种训练方法都采用的,我们可以用MLE 极大似然估计
似然函数如下图:
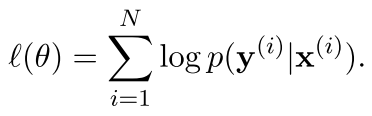
所以我们现在可以把上面的这个东西给再变换一下,变成一种联合的分布
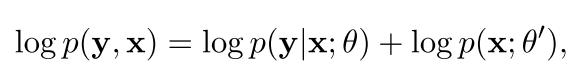
这样也可以看作让整体的似然函数最大,但是一般我们有了一个输入之后,我们的右边的参数不会影响我们的左边的参数,所以一般都是只有第一个参数起作用。
现在我们看看条件随机场的似然函数是什么形式:
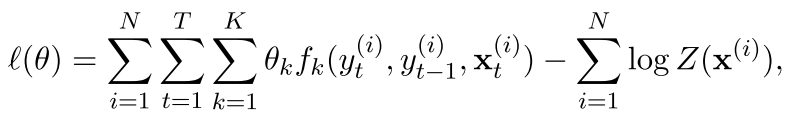
为了让那些权值比较大的参数稍微小点,我们接着这样的定义
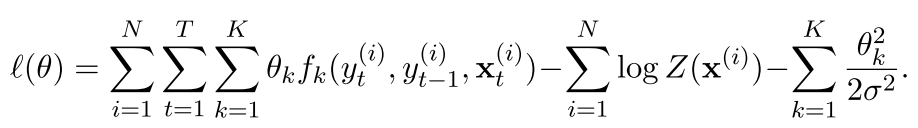
这个是加了L2约束的 不细讲
有时候也会加L1约束,这种约束有下面这样的形式
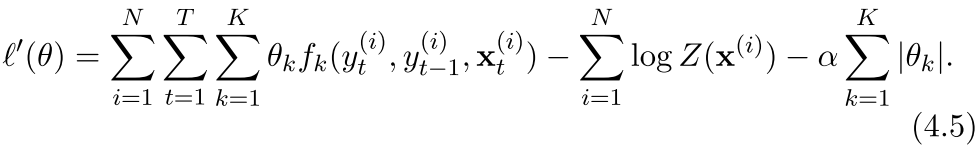
作用是feature selection 不细讲
现在我们看看 求导后变成了什么
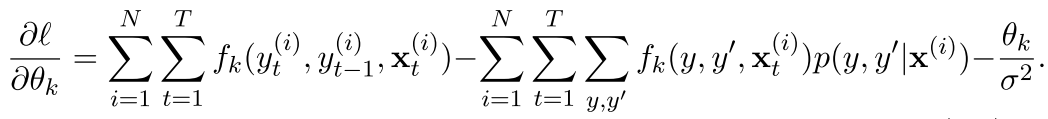
--(3)
可以看出来右边第二项确实是所有的y,y' 需要遍历一遍,所以我们,这样其实就是看看最后x出现了多少次而已,注意其中的xit是指的第i个样本的第t个观测量
所以就是xt的期望。这个可以在整个数据统计出来
第一项是这个fk出现的次数,在整个样本空间里面,的期望,也就是
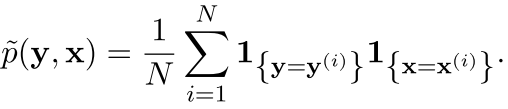
可以看出来,这个其实就是整体的期望分布,所以我们的这个东西可以看作是一个经验分布和样本分布的对称,是让样本分布和经验分布一样(导数等于0,没有约束项)
我们在训练的时候,往往这种在整个样本空间进行训练的方法很不靠谱,因为这种方法一般都是二阶的技术 ,比如L-BFGS
现在我们再换一种思路,考虑一下
online learning 也就是在神经网络里面特别流行的SGD:它和以前的比较可以用下面这个来说明
the directions of the individual steps may be much better in L-BFGS than in SGD, but the SGD directions can be computed much faster
对于SGD来说,每一次的梯度(对于某一个特征) 是这样的
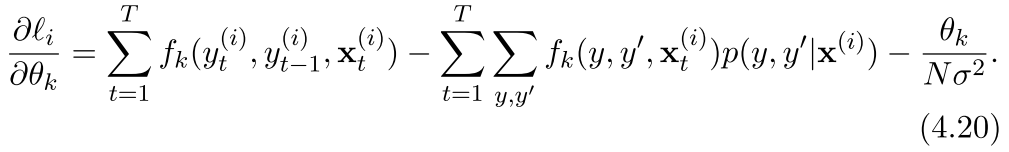
现在的更新过程就是这样的了
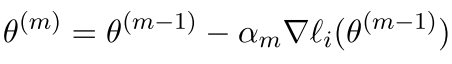
也就是每次更新一小部分,注意我们这里更新的是某一个参数
一般而言,我们的这个更新过程有下面这个形式:
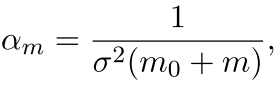
也就是我们的更新过程中学习速率是不断变化的,当然我们可以采用其他的方法 ,如adadelta等等
========================================================
现在我们的参数有了,就该下一步开始在测试的时候推理了
推论
现在我们的模型有了,看看我们怎么在测试的时候进行推理
我们首先看看前向和后向传播的表达式是什么样子的
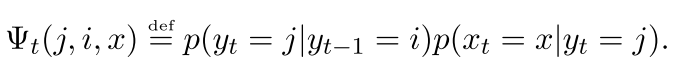
这是一个状态转移概率,定义为一个三个变量的转移概率
所以在标准的HMM中,整体的概率有
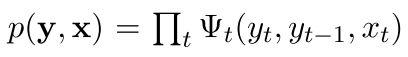
然后我们现在把整体x的概率表示出来
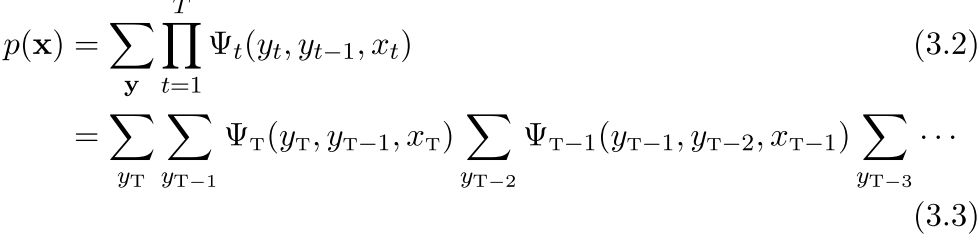
所以我们可以看出来这个东西其实就是不断的往前传递
注意每一步都是求和,因为最终的是看x 仅仅x是我们要求的概率
现在开始定义前向传播的概率
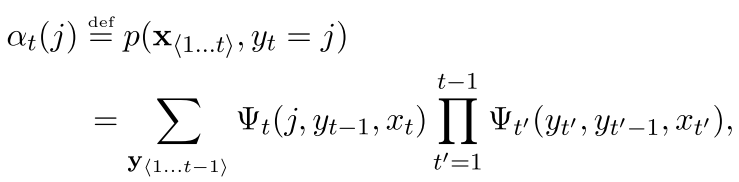
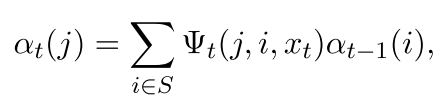
可以看出来 ,前向传播就是到这个时刻t,当前的y是j的概率,他是以前所有的可能性到这里的之和,因为我们现在不考虑前一个时刻的状态,所以事情变得比较直观
所以第一个时刻的状态就是
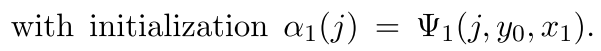
其中y0是我们初始化的一个变量
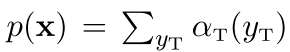
然后我们看看后向传播的样子
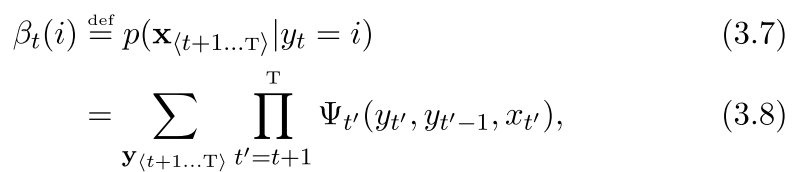
也很可爱是不是
所以也是有
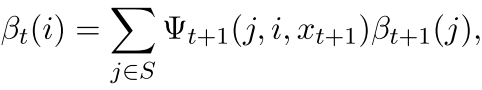
所以我们还是这样的往后推,但是我们这个由于是后向的,所以有
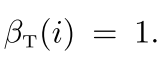
(注意我们只有开始符号没有结束符号)
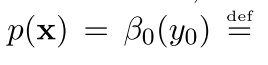
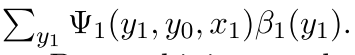
所以我们的这个过程可以看作是一个前向和后向综合在一起的过程,在上面参数推导(公式3)的时候我们看到为了得到一个参数的梯度,我们得有下面的这个概率
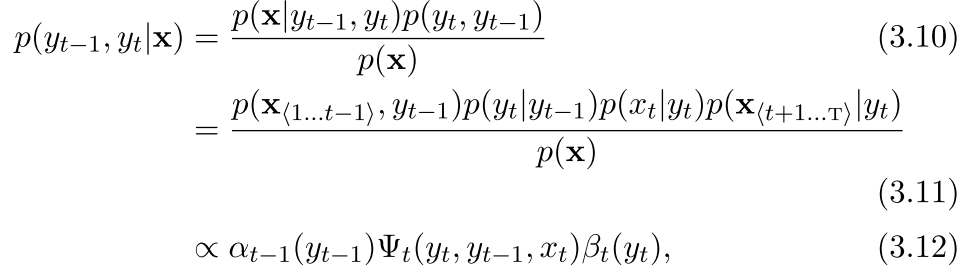
注意上面公式在推导的时候3.10可以不要其实
然后我们可以看到其实3.12比3.11少的就是那个p(x)
现在看看怎么进行推理
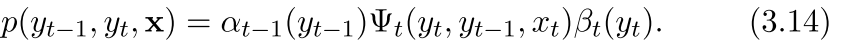
有了这个之后,我们便可以继续往下走,
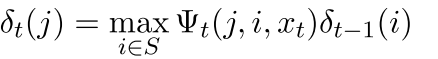
可以看出来这个是我们的viterbi算法
现在我们返回到CRF
在我们的CRF中,目标函数是这样
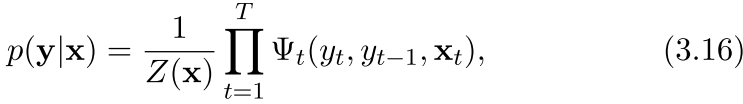
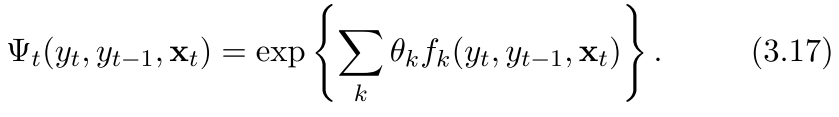
所以可以看到,在CRF中分母没怎么变化,但是我们的分子只不过从HM里面的p(x)变成了z(x) 也就是一个统一的形式,而不是概率的形式,因为我们的分母不是概率了,我们的转移的3.17是一个指数函数的形式
=====================================================================
这次就写到这里,下次估计还会加一个关于这个CRF程序的东西,我们下次再讲 2016-05-09(中午)
回复列表: