这篇文章是关于卷积矩阵低维分解的

--------------------------------------

我们传统的CNN就是有一点问题是卷积矩阵太大，因而无法得到相应的参数，所以我们经常需要对矩阵进行低维度分解来得到正确的表达

传统上我们的卷积矩阵是一个四维的张量，W ∈ R^N×d×d×C 表明输出是n个label  输入有C个（一般指batch的输入或者图像里面的通道数） 然后d*d是指的我们的卷积核的大小

对于一个输入的feature map（可能就是一个图像） 我们的矩阵可以表示为 Z ∈ R^X×Y ×C be the input feature map.

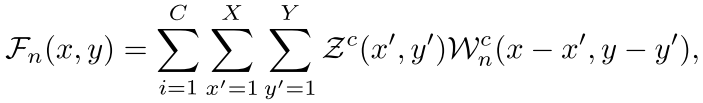  这就是我们的输出

The goal is to find an approximation W' of W that facilitates more efficient computation while maintaining the classification accuracy of the CNN

作者提出了下面这个约束目标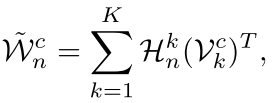 

也就是我们的这个每一个filter（d*d）就是由两个低维向量的外积，然后我们的构造K个这样的向量对，就可以得到了我们的一个low rank的逼近，因为每一个外积的rank

为1，所以K个就可能是K

有了这个 我们就可以对最上面那个式子重新进行处理了

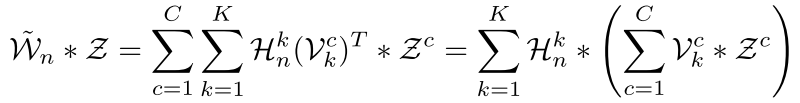
我们可以看一下这样做的好处

============================

仅仅通过原始的卷积操作 也就是最上面的那个式子 复杂度是 O(ddNCXY )

但是现在我们的复杂度变了 因为向量外积操作复杂度会很低 所以我们的模型就变成了

 O(dK(N + C)XY ) 如果选择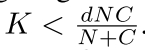  那么肯定会降低很多复杂度

==================================================

但是低维逼近的还有一个非常重要的作用是当原模型训练出来后以后再应用的时候用一个低维的操作区逼近

所以作者提出了下面的这个目标

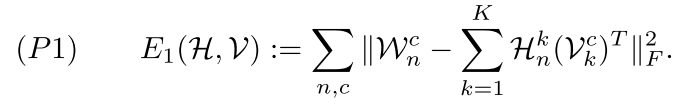
我们可以看到其实就是对我们的原始张量首先进行一个空间变换变成一个矩阵，然后我们对剩下的这个矩阵进行svd变换得到了我们的这个目标的参数，然后我们得到了H

和v，就是我们的卷积的参数

=====================如果直接用这个新的卷积参数去训练我们的这个对象，那么我们的模型可以看成

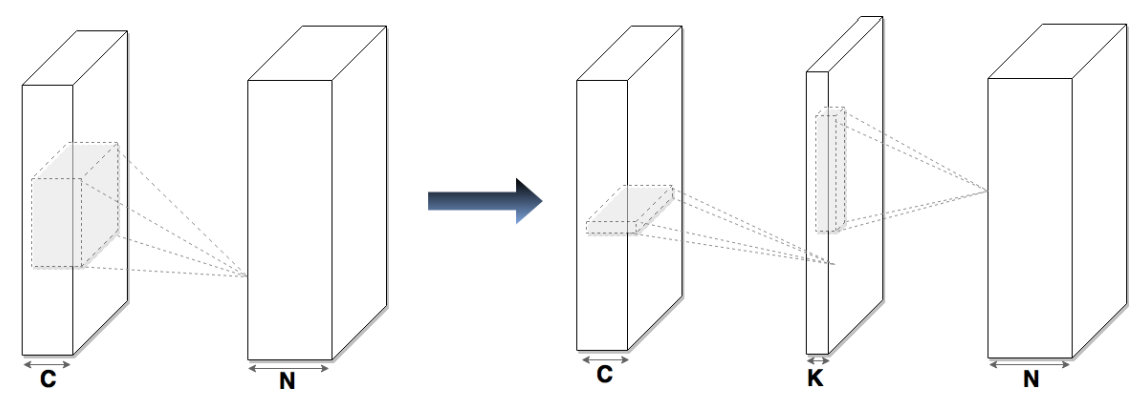
左边是原始的 右边是我们降低维度之后的方法，这种方法可以看出来是两步走，不是取一片了（d*d）而是将先横着着取一下，再竖着取一下，这种方法是一种叫做

As each convolutional layer is parametrized as the composition of two convolutional layers, the resulting CNN has more layers than the original one.

Although the effective depth of the new CNN is not increased, the additional layers make numerical optimization much more challenging due to exploding and vanishing gradients, especially for large networks. To handle this problem, we use a recent technique called Batch Normalization (BN)

==============================

最后作者将自己的代码公开了

lowrankcnn-master.zip