fe80::8dae:e796:a2d7:8fb2%12
这个文章比较牛逼,是最近两年出来的 关于神经网络优化的文章
首先我们的目标函数是:
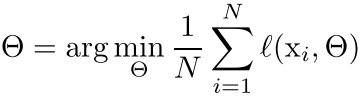
然后我们的标准batch gradient是;
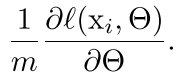
但是这种标准的batch有点不好,就是容易陷入局部最优解,因为每次都是在一个小样本上面
Fixed distribution of inputs to a sub-network would have positive consequences for the layers outside the subnetwork, as well. Consider a layer with a sigmoid activation function z = g(W u + b) where u is the layer input,the weight matrix W and bias vector b are the layer parameters to be learned,increases, g ′ (x) tends to zero. This means that for all dimensions of x = W u+b except those with small absolute values, the gradient flowing down to u will vanish and the model will train slowly. However, since x is affected by W, b and the parameters of all the layers below, changes to those parameters during training will likely move many dimensions of x into the saturated regime of the non-linearity and slow down the convergence. This effect is amplified as the network depth increases.
也就是当我们每一层的输入如果不处理的话,那么这一层的导数有可能为0或者变得非常大,这样不太好,所以我们必须对每一层的输入也进行标准化
We define Internal Covariate Shift as the change in the distribution of network activations due to the change in network parameters during training.
就是我们的输入的分布随着我们的参数而发生改变,就是输入经过一层,分布已经变化了,而我们不想看到这种变化,因为我们的deep learning随着网络的更深层,应该是对分布更好的进行建模。
所以作者提出了:Normalization via Mini-Batch Statistics
对于网络中任意一层,假设有d维,则我们对其中的输入进行标准化得到:
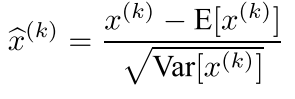
其中x^(k)是这一层这一维的输入,而均值和方差都是在这个维度的m个mini-batch上面展开的
所以这样会使我们的网络的收敛速度特别快
但是这样对每一层的输入标准化之后会有一个问题,那就是我们每一层的表达能力会下降,比如说:normalizing the inputs of a sigmoid would constrain them to the linear regime of the nonlinearity.
就是当我们的输入标准化之后他在sigmoid里面出来后就是线性的了 所以这样也不行,我们就得再做一次改变,加两个参数:
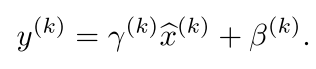
最后的算法就是:


我们现在只是把我们的在训练的时候的输入给标准化了,但是在inference的时候,这样以一个batch 来标准化并不见得是什么好的选择,因此我们需要对这个进行改变,就是在
inference的时候我们的输入就不是以这个batch的均值还有方法来标准化了,而是整个训练集的mini-batch的均值,就是整体均值的无偏估计
回复列表: