又是一个大神作  里面的数学真心让人哭

==========================================

首先看看作者提出的动机，

reduced transparency and discriminativeness of the features learned at hidden layers:隐含层的可判别性太低，往往都是很随机的一系列表达

纯的动机就是：

We are motivated by the following simple observation: in general, a discriminative classifier trained on highly discriminative features will display better performance than a discriminative classifier trained on less discriminative features.就是一个判别性越好的特征会比判别性不好的特征对于最后的分类表达来说是好的，

所以我们需要对这些隐含的东西进行处理，表达出其中可以判别的东西，

我们看看那DSN的表示是什么：

假设原始的表达是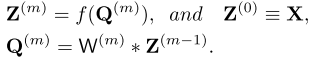：，X表示输入，其中Q表示输入经过一次变换之后的表达，在CNN里面就是一个对于前一个输入的卷积表达，Z表示的是经过pooling之后的表达，f一般表示这个pooling的方法，m表示层数

最后的这个东西我们的参数表达就是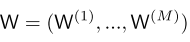

现在，我们加入我们自己的另外一套参数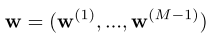，其实就是一个线性分类器，比如SVM或者logistic回归的东西，

我们现在对于我们以前的目标进行，更改，不仅仅是在最后的输出层计算误差了。而是加入了一个新的目标

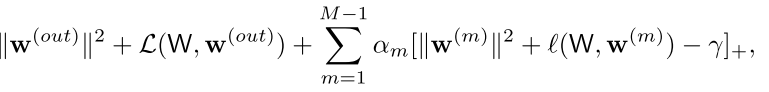
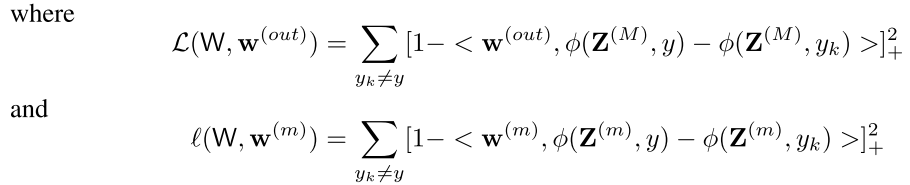
这个是标准svm的判别，其中最左边的两个是原始的svm的目标函数（为了简单起见去掉了惩罚相C）

而右边一项是对每一层的判别能力的检验，也就是每一层都可以看做最后的输出层，然后对于每一层给个svm判断这个特征的表达是否合理，

这个方法中右边的那一项有一个γ是为了表示隐含层每一层我们只要让他的误差小于一个数，那么我们就可以把这一层当成比较discriminant的

（但是我感觉越往上应该区分能力越强，所以这个γ应该也是跟我们的层数有关）

然后前面的α m表示的是我们对于这个隐含层判别能力的权重