又是一个深度学习的东西,就是根据名字也能看出来就是deep learning里面隐含层的数目不一样
====================================
首先我们看一下 Residual Networks (ResNets) 是什么样子
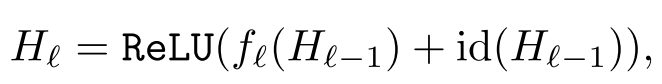
模型是这样 就是每一层除了由原本的输入 也就是Hl-1现在再加上一个原来的映射 也就是id(indentity mapping)
它的示意图是这样的
这样做的一个好处就是 我们知道在线性回归里面(ESL第三章前一部分)讲了很多用残差(Residual)来拟合线性模型的东西 也就是对于一个输入x 我们学到一个
函数f(x)最能将f(x)映射到y 现在我们不这样了 而是把f(x)-x当作目标 就是一直让这个目标减小
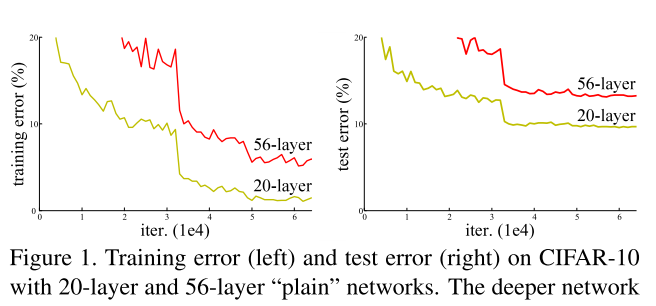
作者提出这个东西的原因是:本来我们深度学习模型随着网络层数的加深,应该是越来越能够拟合出好的这种映射函数(最差的情况下,新增的层全是id也就是直接映射层,那么也应该和以前的一模一样)但是在实际情况中发现并不是这样,随着网络层数的加深 模型的效果反而不如以前
针对这个问题,作者的一个假设如下:
The degradation problem suggests that the solvers might have difficulties in approximating identity mappings by multiple nonlinear layers. With the residual learning reformulation, if identity mappings are optimal, the solvers may simply drive the weights of the multiple nonlinear layers toward zero to approach identity mappings.
也就是我们强行的把某些层加入到id 这样的话会使这种线性的表达更强
=======================================================
好了 介绍完 ResNets之后 我们开始研究下一个,也就是本文的重点 随机层数的网络
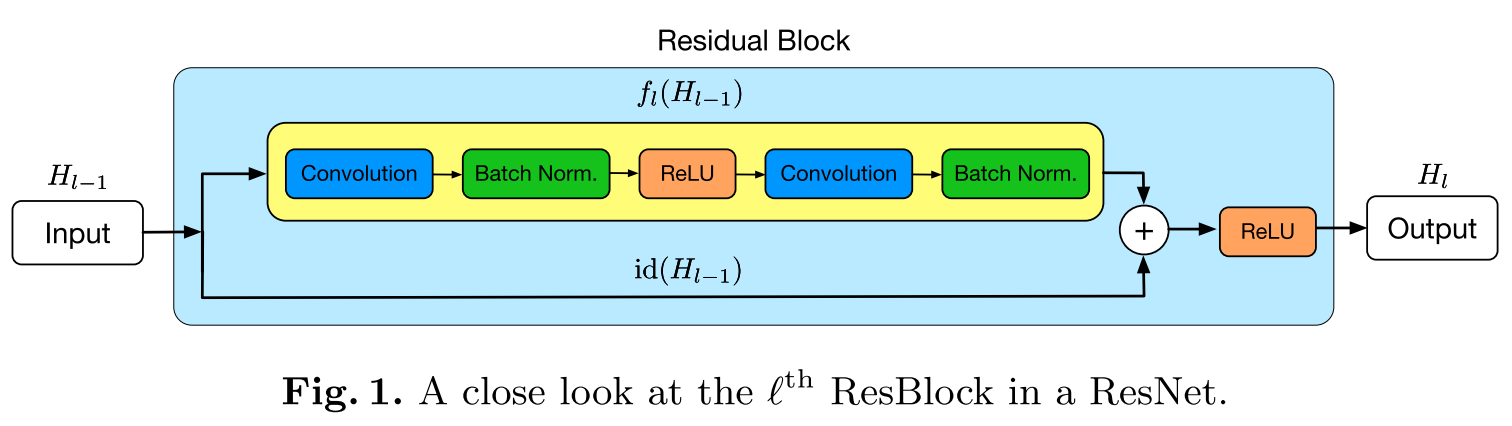
它的主要结构如下图所示:
可以看到 就是标准的ResNets 但是其中的非线性部分被随机的(就像dropout里面的伯努利分布一样)被取消掉,也就是这一层只是纯线性的
现在的公式可以表达为:
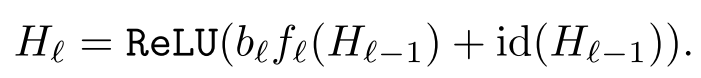
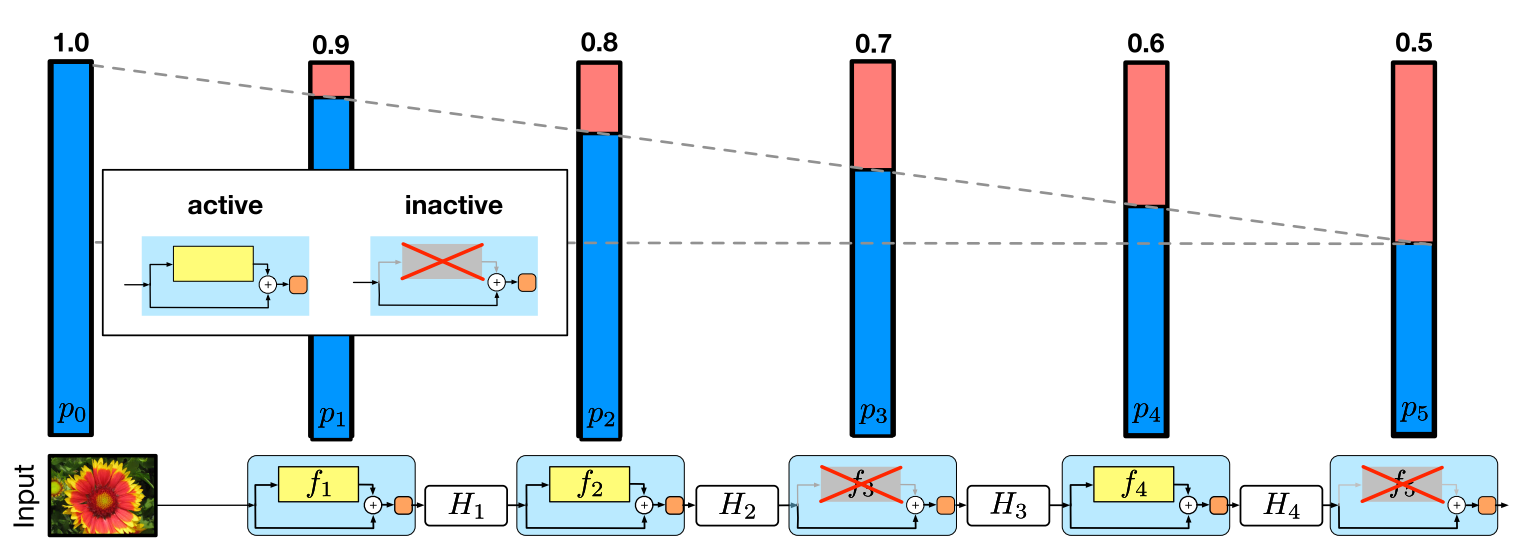
其中的bl是0或者1 其中的每一层按下面这个概率被bypass
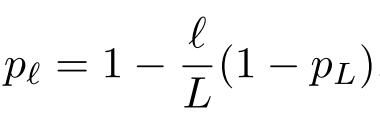
其中pL是一个预定义的值 小l是从输入数到输出的层数 所以输入的时候l为0 最后pl非常大 不会被drop 但是越到后来 越容易被drop了
The linearly decaying survival probability originates from our intuition that the earlier layers extract low-level features that will be used by later layers and should therefore be more reliably present.
最后的pl是设的为0.5
我们知道dropou在训练的时候也是随机drop 但是在测试的时候每一个神经元是要乘以那个系数的(因为在训练的时候每一个被训练的神经元使得劲非常大才能使全体效果这样 现在大家都来了那么每个人不用使那么大的劲了)
测试的时候系统的表达是这样
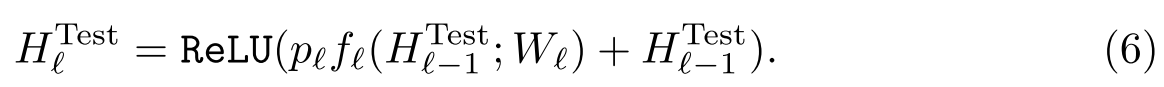
From the model ensemble perspective, the update rule (6) can be interpreted as combining all possible networks into a single test architecture, in which each layer is weighted by its survival probability.
最后的实验是标准的图像里面的那几个数据集
作者还做了一个检测 vanishing的实验
就是看看误差反传到第一层的时候看看还剩多少 是不是vanish了(也就是基本上没有了)
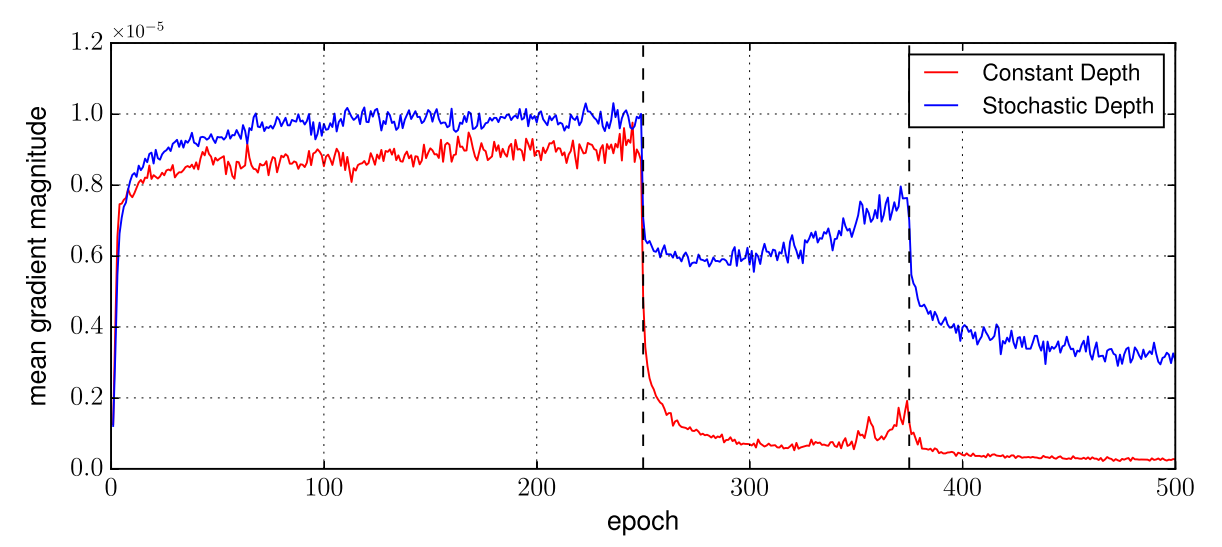
可以看到蓝线确实是比较好 还是有误差的
(但是我感觉这个应该跟有一篇在递归神经网络里面检查LSTM的作用一样 不仅仅看第一层的误差的绝对值 而是看它和最外层(输出层)误差的比值)
实验代码在下面:
回复列表: