这个工作主要是在选择我们的激活函数上面

=====================================================

首先以前的激活函数都是这样的，在两端会饱和 比如sigmoid 或者tanh  在我们的输入很大的时候会饱和 这个很让人苦恼，因为饱和了，导数基本上就为0  基本上误差就不会动了，作者在这个文章中提出了两个东西

也就是 以前虽然我们在RNN里面加了很多gate什么的，但是我们并没有消除这种饱和带来的不好，并且我们很难确定这种饱和，也就是非常难的hard decision where to clip this error

但是我们还可以加入一些噪声来搞定 来来来 我们看怎么弄的

An activation function h(x) with derivative h0(x) is said to right (resp. left) saturate if its limit as x → ∞ (resp. x → −∞) is zero. An activation function is said to saturate (without qualification) if it both left and right saturates.

现在我们定一下 什么叫做hard saturation

也就是设置我们的一个常数c，当x>c或者x<-c的时候，h'(x)=0 这种叫做hard饱和，也就是直到那个地方才饱和出来

作者在这个工作里面定义了两个hard function

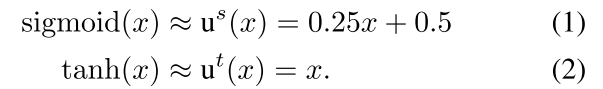
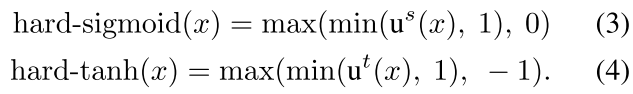
作者为了hard，就把所有的函数弄成线性的，也就是一阶泰勒展开，这样可以保证一阶线性。

我们的函数的导数现在是这样的

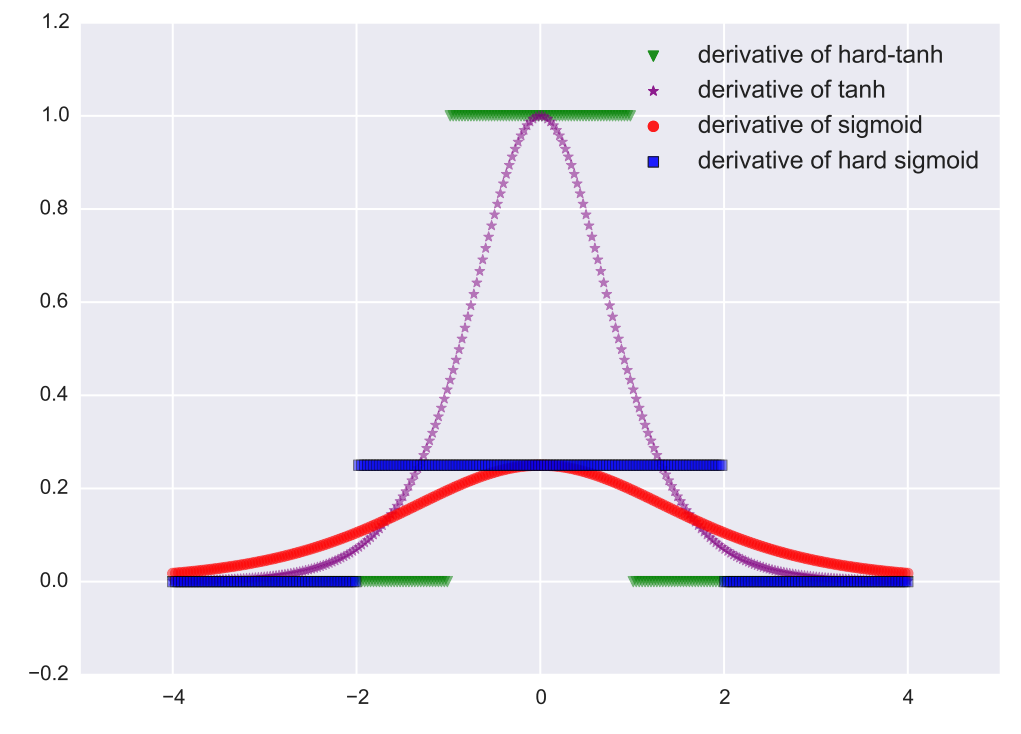
以往的sigmoid和tanh函数会在0-1之间有很大的导数，然后把当前的值扔到很远，但是扔远了之后导数又小了，所以回不来了，得花好长时间才能回来。

退火（anneal）指的是不断减小某个参数的值直到0 举个例子

在作者这个工作中，我们对每个函数加了一个随机的噪声

Let ξ have variance σ 2 and mean 0. We want to characterize what happens as we gradually anneal the noise, going from large noise levels (σ → ∞) to no noise at all (σ → 0).

并且这个函数有以下特征

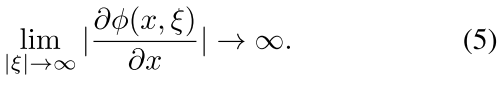
也就是当x在很两端的时候导数很大，这样可以把现在的x（拉回来）

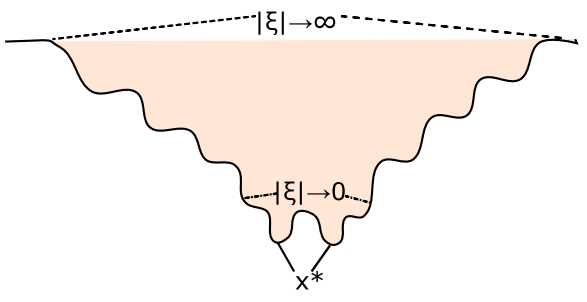
这就是退火的过程，逐步拉回来（从上面到下面）

现在看作者怎么把这个噪声的激活函数加进去的

the amount of noise added to the nonlinearity is proportional to the magnitude of saturation of the nonlinearity

现在的激活函数有下面这样的形式：

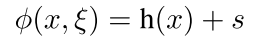
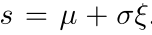
Here ξ is an iid random variable drawn from some generating distribution 其中h（x）是指的原始的激活函数 sigmoid 或者tanh啥的

为了使我们的激活函数是无偏的，不会改变以前激活函数的统计特性，所以作者有一个指导思想就是：

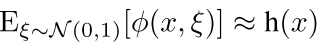
而且作者想了一个来使噪声饱和区很大，但是在非饱和区很小的方法

首先定义：

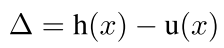
也就是原函数和hard函数的差距，其中的u（x）是一阶泰勒展开可能会很大

所以作者这样的定义之后，我们就有：

The quantity Δ is zero in the unsaturated regime, and when h saturates it grows proportionally to the distance between |x| and the saturation threshold x t . We also refer |Δ| as the magnitude of the saturation.

好了 现在 我们为了得到上面式子中的那个σ，现在可以这样的做：

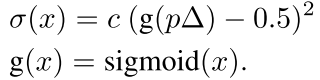
因为我们的目的是，当Δ小的时候，说明在饱和区，然后我们的这个σ也应该小，所以我们这个sigmoid就在0,5附近，但是当到两边的时候，sigmoid在0或者1，所以这个σ也很大，噪声起作用的比较明显。

并且对于导数，当在两端的时候，也就是饱和的时候，

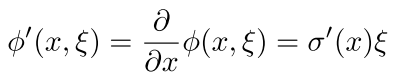
which is non-zero almost surely.

可以看到 当在非饱和区的时候

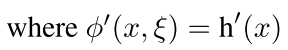
 Pushing Activations towards Linear Regime

上面的那种方法，由于我们的程序里面噪声可能有正有负。所以在饱和的时候如果ga一下啊来了一个往外偏的噪声，所以我们需要对这个方向来进行处理：

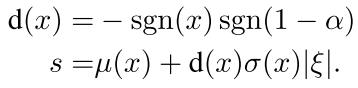
所以现在你看s给加了进去，就是确定这个方向的，现在

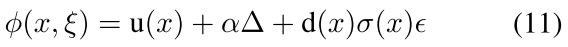
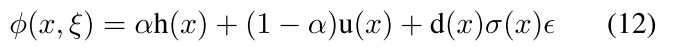
注意这个里面的 

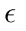= |ξ|

因为这个里面u(x)可能很大，所以当a大于1的时候，还是得反过来。

这样，我们的这个噪声总是让这个最后的东西满足在0-1之间，而且都是可导的

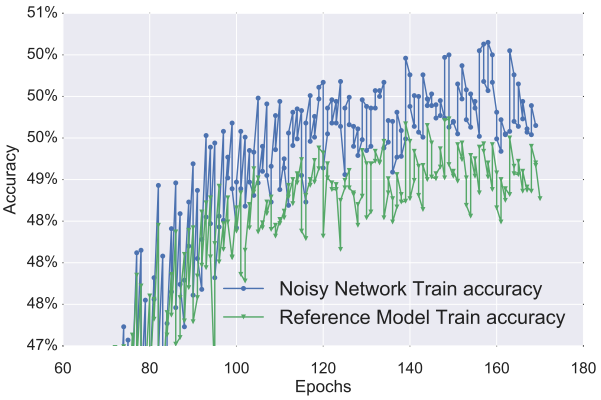
最后的效果确实不错

这篇文章还放出了好多code 也就是 Learning to Execute一个 https://github.com/wojciechz/learning_to_execute

Penntreebank Experiments 语言模型的  用的LSTM在这 https://github.com/wojzaremba/lstm

Neural Machine Translation Experiments  https://github.com/kyunghyuncho/dl4mt-material

Image Caption Generation Experiments  https://github.com/kelvinxu/arctic-captions

这个工作的代码在下面 是用 Theano写的  回头好好研究研究 noisy_units-master.zip