今天读的这个文章还不错(最起码比下午的variational inference要牛逼一点)
------------------------------------------
A function is said Lipschitz continuous if it takes similar values on points that are close. More precisely, the slope of the function is bounded by a constant that is independent of the choice of points.
也就是这个函数的导数或者梯度是有范围的
所以像x^2这种函数就不是 Lipschitz continuous因为这个东西的导数在整个样本空间里面当x趋于无穷的时候slope是无穷的
所以现在考虑这种
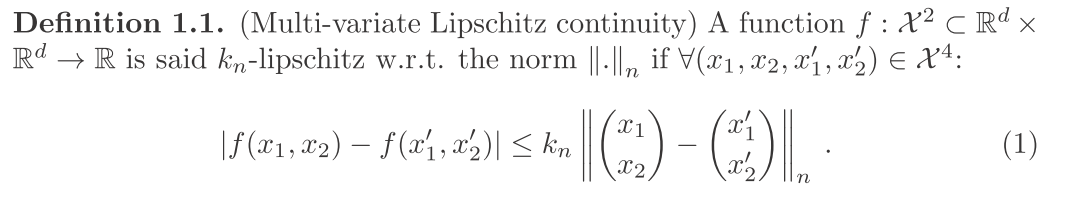
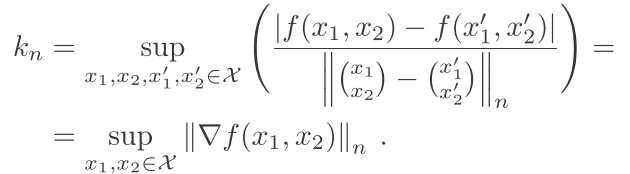
然后进入正题,首先我们有一个马氏距离函数,可以这样看
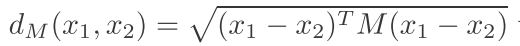
对于这个:
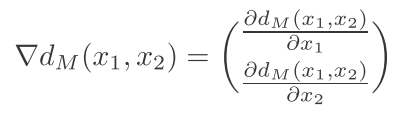
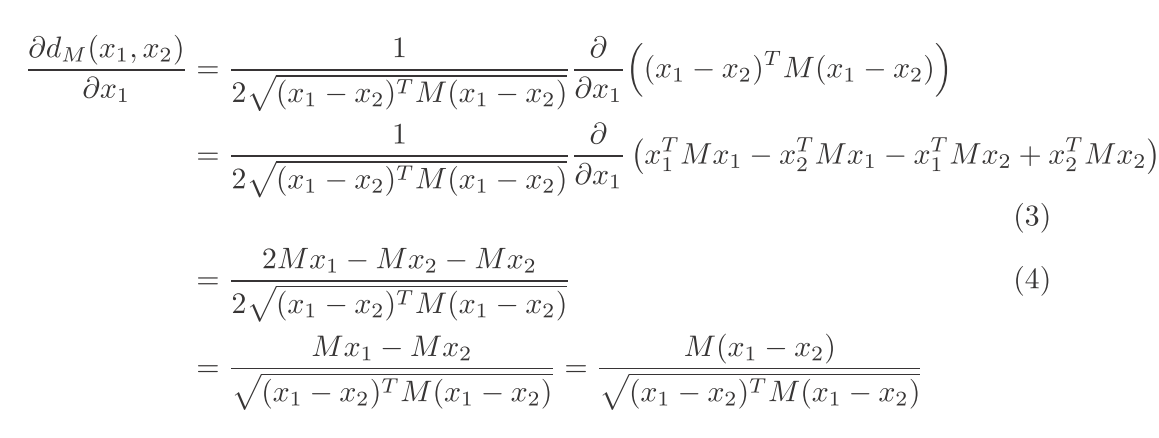
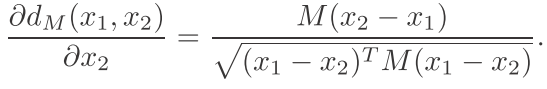
然后我们看看这个函数的k-lipschitz是多少:

注意其中用到了 Cauchy-Schwarz inequality (|AB|<|A|.|B|)
Cholesky decomposition M = L T L
可以看到这个东西也是有限维度的
再来看看双线性函数
d(x1,x2)=x1TMx2
其中中间的M是一个映射矩阵
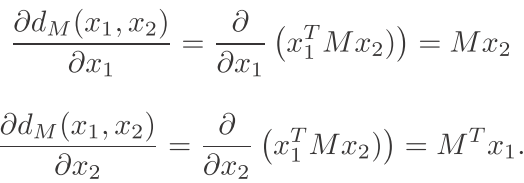
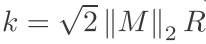
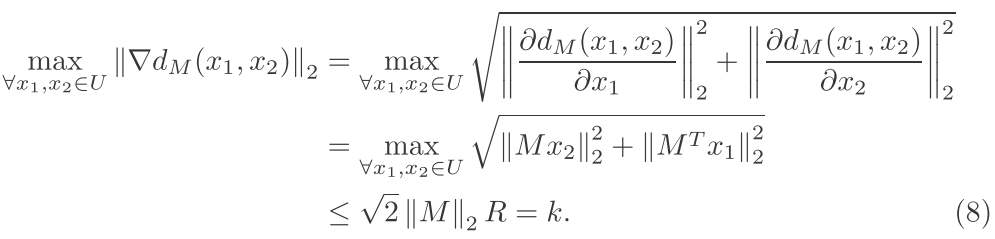
回复列表: