首先看看一般的优化问题：

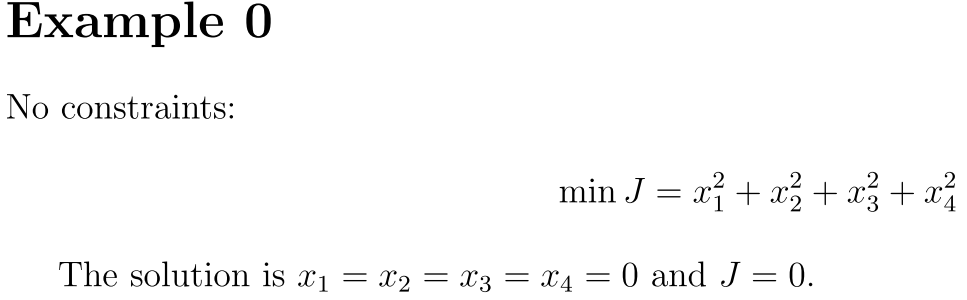
对于这种问题，我们不用什么约束条件，直接求导就行。

然后现在有了一个等式约束，

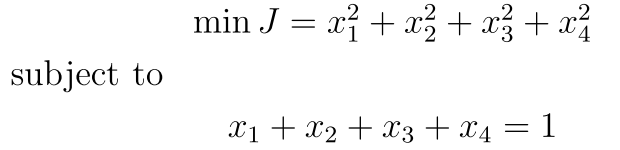
我们可以把问题转化为：

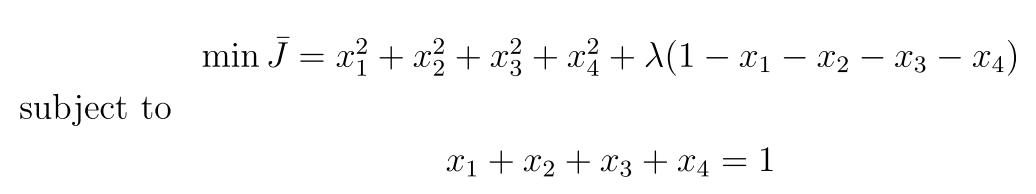
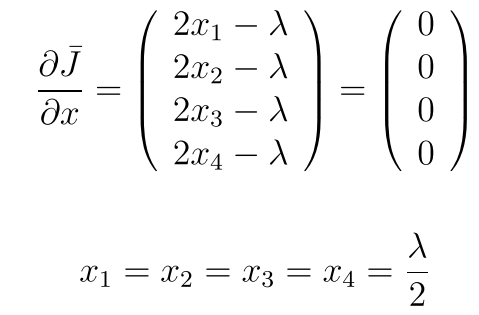
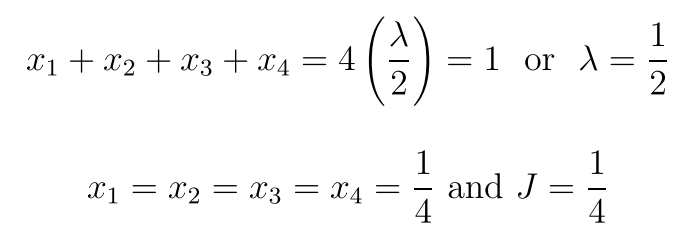
它的图像是这样的

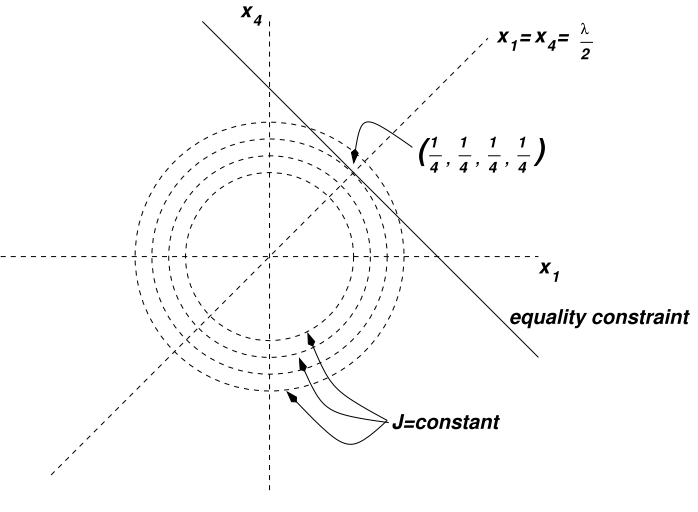
现在看看最难的

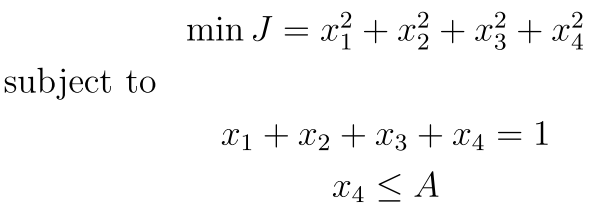
这个就有点麻烦了  呵呵

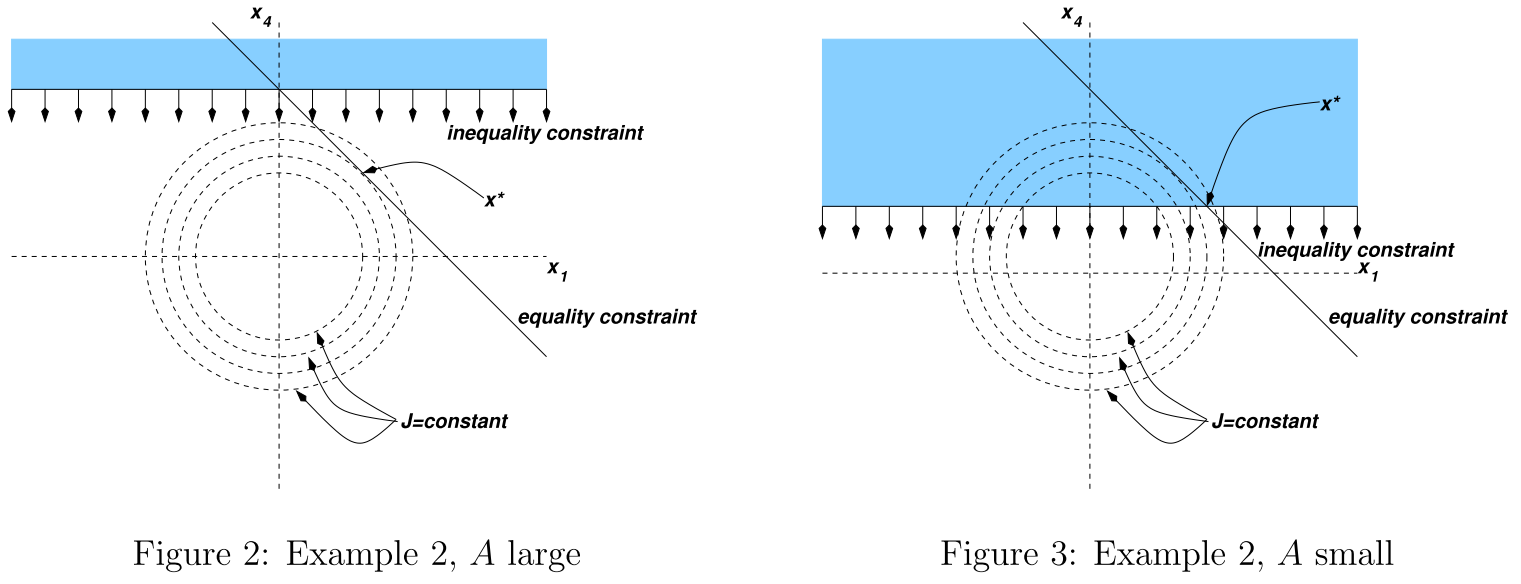
其中蓝色的部分是forbidden area

然后对于左边的 当A很大的时候，我们可以不用管他 但是现在当A很小的时候，我们就要考虑了

首先，我们考虑一个降低难度的问题：

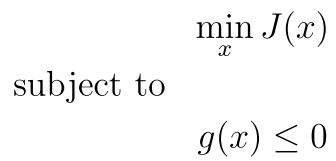
并且假设我们已经有了一个最优解 则

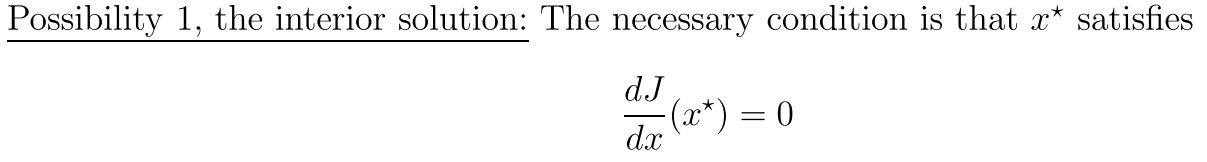
然后对于第二种当A比较小的时候，我们会有这样的一个目标

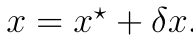
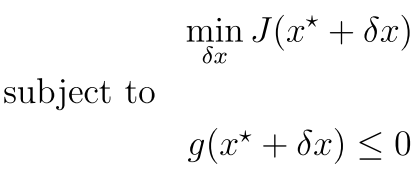
当我们的这个乘子很小的时候small �x

然后我们就可以说确实这个也是满足的 因为基本上逼近于原方程

所以 现在 我们做一阶泰勒展开

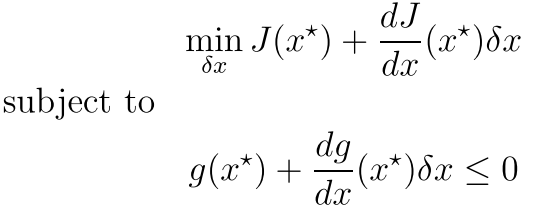
这样的方程还是满足的  而且以前的最优解x*和现在的新加的x没有什么关系，所以下一步就有

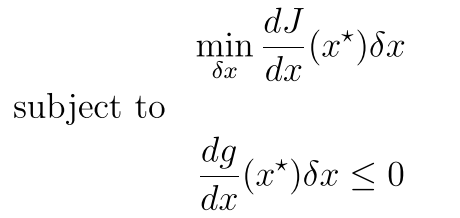
公式8就是上面那个式子  所以现在 这个问题变成了一个整数线性规划的问题了

现在我们考虑

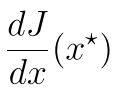
的不同符号状态对最终结果的影响

如果它大于0  那么

这个的最优解也就是

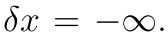
同理：

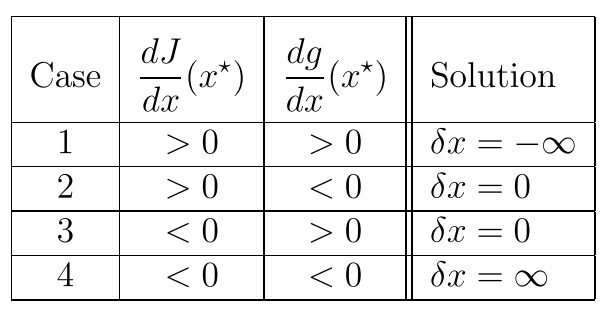
可以看到最终还是有四种情况的 其中能使

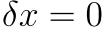
的清空只有2 3

也就是这两位的符号必须相反

所以 现在定义一个正数u 他使我们的方程变成：

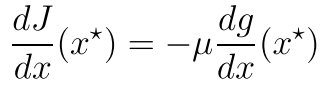
所以现在我们再看看

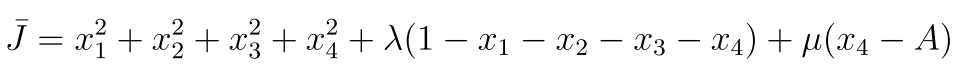
我们还是先求导:

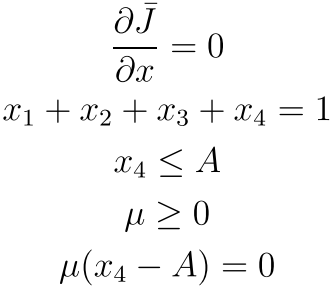
其中最后一个是为了满足现在的方程和原方程的最优解一样

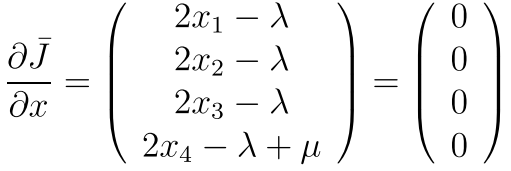
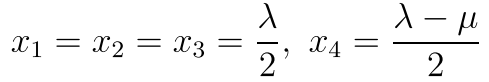
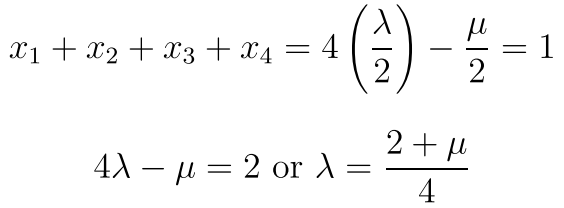
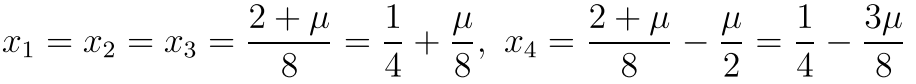
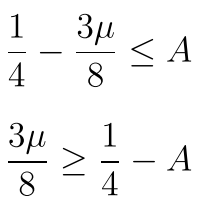
所以现在我们分析 一下啊 如果A>1/4 那么直接是约束没什么用 但是我们需要看看所有的方程是否都满足

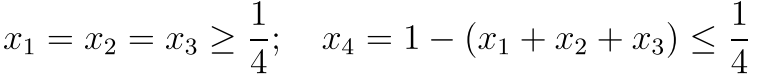
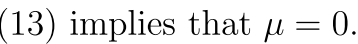
所以最后

-------------

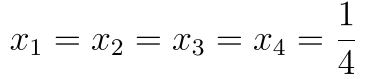
看看当A<1/4的时候哈 这样13 会让u=0 但是这样不行 因为有一个约束被否定了 所以x4=A

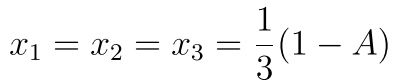
所以 我们知道

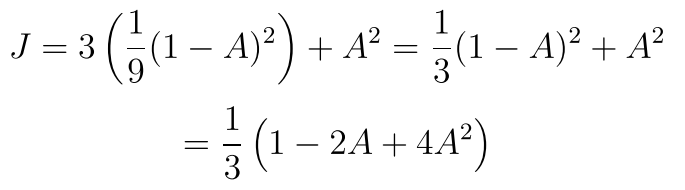
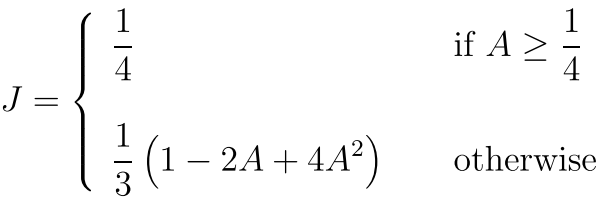
很好吧 

===================================

最后附上来两个文件：

MIT2_854F10_kkt_ex.pdf
16-kkt.pdf