这个工作我感觉也一般

===============================

主要就是讲半监督的来进行图的embedding的

这个工作的主要特点是在图上做采样 不像以前我们词向量一样在句子中做上下文的采样

首先 看看半监督的过程

半监督分为transductive 和 inductive  也就是直推式和递推式 也就是一个可以直接推导出来还有一个得慢慢的通过隐含条件推导出来

首先  这种方法的一般形式为

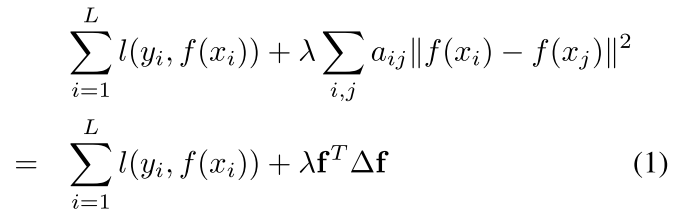
也就是 有监督的数据 1-L 还有非监督的数据L-L+U

其中上面这个式子左边的第一部分是让我们的模型（f）在监督数据上面表现的最好

右边的式子是让我们的所有数据（有标签和无标签的）最后的输出和他们的样本相似度aij相同，也就是相近的样本（aij小）则他们预测的label应该也相近

这种约束叫做拉普拉斯约束 （ Laplacian regularization）

最近几年 现在的这种惩罚项（也就是看输出的相似度）已经不是特别流行了 现在的就是让两个样本的embedding比较相近

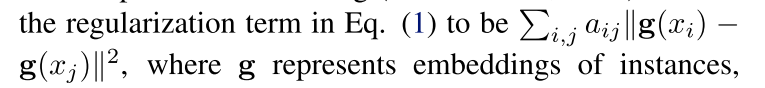
可以看到现在不仅仅是让最后的预测输出相近了

where g represents embeddings of instances, which can be the output labels, hidden layers or auxiliary embeddings in a neural network.

这样的更加抽象

 作者对以往的工作进行了总结

可以看到没有最后一个是把所有的都考虑进去的

==========================================

首先看看我们上面式子1 的第二部分怎么优化 刚才那个式子和我们的词向量很像 也就是CBOW和skip-gram 也就是上面的式子（1）中右边的aij是是否我上下文出现这个词

那么作者在这里做的就是这样

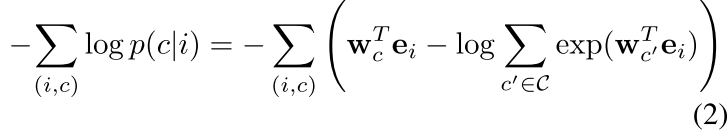
也就是在图上 让我更能很好的预测我周围的样本  其中c是指的context e是我们的embedding

那么在图上我们怎么像miklov的negative sampling一样在上下文进行采样呢？可以看到我们试一下这种方法:

其中的r1和r2是我们预先设定的参数 d是预先设定的窗口大小

==============================================

先看看直推式的 Transductive Formulation

在这个里面 我们的有监督的部分不仅仅是feature了 还有一个样本中的embedding 也就是词向量一类的东西，我们把它和元特征拼在一起生成label y

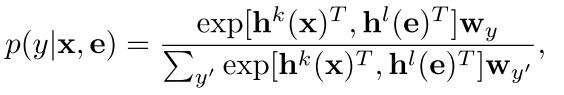
然后 我们的训练目标就变成这样了

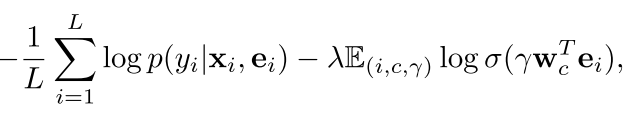
可以看到右边还是那个结构预测（非监督的部分） 和miklov的一样 是看内积的大小

但是这种方法有一个不好就是我们的这个embeddeing必须是训练样本中出现过的 我们才能结合在一起得到训练的label y 举个例子 就是我们的feature x可能是没有在训练样本中直接出现过，但是他的embedding（或者子部分的embedding）必须出现过 所以这样没有出现过的embedding就没法来搞了

来看看它的训练步骤 是分两步的

==================================================

递推式Inductive Formulation

在这种方法里面 我们的每一个embedding不是预先设定好的 像词向量一样一个词给一个 而是由输入特征给出来的 比如

we apply k layers on the input feature vector x to obtain h k (x). However, rather than using a “free” embedding, we apply l 1 layers on the in- put feature vector x and define it as the embedding e = h l 1 (x). Then another l 2 layers are applied on the em- bedding h l 2 (e) = h l 2 (h l 1 (x)),

也就是 我们每次都是从隐含层中抽出来一层当作这个输入的embedding

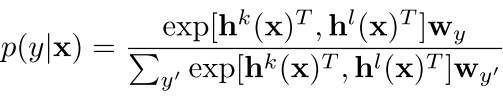
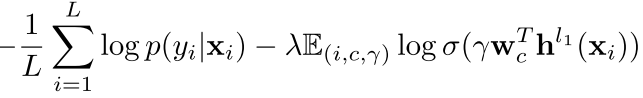
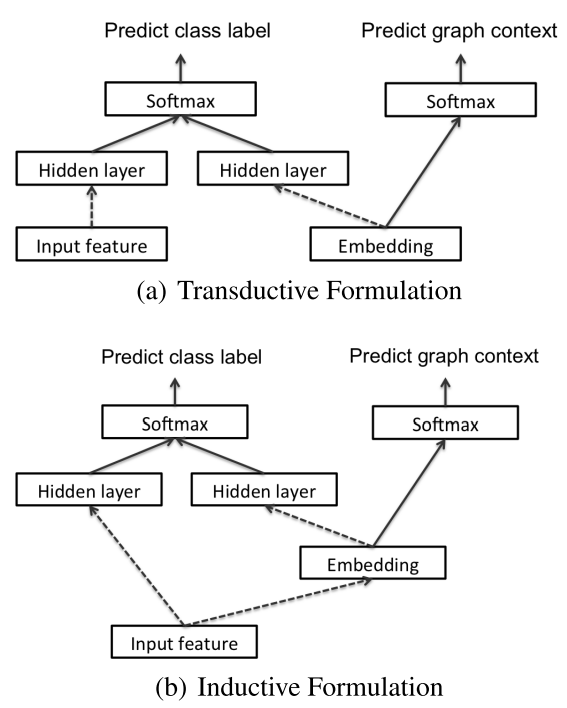
来看看两种model的图示

实验不讲了 作者在很多数据上面跑了实验 但是我脑洞比较大 感觉可以做的非常多